/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 25 lutego 2017 Czas pracy: 170 minut
Zadania zamknięte
Liczba  jest przybliżeniem z niedomiarem liczby
jest przybliżeniem z niedomiarem liczby 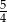 . Błąd względny tego przybliżenia jest równy 2%. Liczba
. Błąd względny tego przybliżenia jest równy 2%. Liczba  jest równa
jest równa
A) 1,225 B) 1,6125 C) 1,2 D) 1,265
Liczba 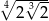 jest równa
jest równa
A) 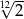 B)
B) 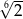 C)
C) 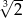 D)
D) 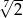
Liczby  i
i  są dodatnie. Liczba
są dodatnie. Liczba 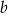 stanowi 96% liczby
stanowi 96% liczby 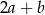 oraz 64% liczby
oraz 64% liczby 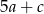 . Wynika stąd, że
. Wynika stąd, że
A) 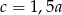 B)
B) 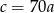 C)
C) 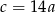 D)
D) 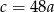
Liczba 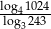 jest równa
jest równa
A) 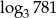 B)
B) 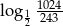 C)
C) 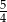 D) 1
D) 1
Najmniejsza wartość wyrażenia 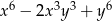 dla
dla 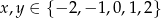 jest równa
jest równa
A) 2 B) 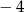 C) 0 D)
C) 0 D) 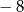
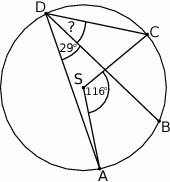
Punkty 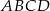 leżą na okręgu o środku
leżą na okręgu o środku 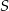 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 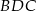 jest równa
jest równa
A) 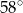 B)
B) 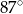 C)
C) 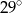 D)
D) 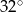
W ciągu geometrycznym rosnącym pierwszy wyraz jest równy 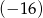 , a siódmy wyraz jest równy
, a siódmy wyraz jest równy 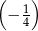 . Kwadrat czwartego wyrazu jest równy
. Kwadrat czwartego wyrazu jest równy
A) 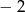 B) 4 C)
B) 4 C) 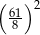 D)
D) 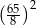
Rozwiązaniem równania 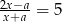 jest
jest 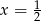 . Zatem
. Zatem
A) 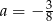 B)
B) 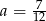 C)
C) 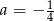 D)
D) 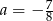
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 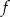 , przy czym
, przy czym 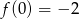 i
i 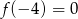 .
.
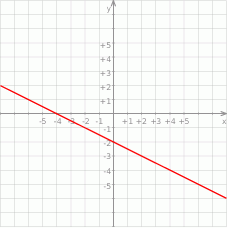
Wykres funkcji 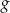 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 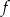 względem prostej
względem prostej 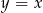 . Funkcja
. Funkcja 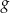 jest określona wzorem
jest określona wzorem
A) 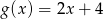 B)
B) 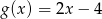 C)
C) 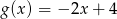 D)
D) 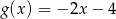
Jeśli funkcja kwadratowa 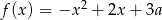 nie ma ani jednego miejsca zerowego, to liczba
nie ma ani jednego miejsca zerowego, to liczba  spełnia warunek
spełnia warunek
A) 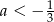 B)
B) 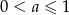 C)
C) 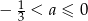 D)
D) 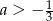
Układ równań 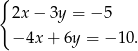
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma nieskończenie wiele rozwiązań
Funkcja 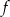 określona jest wzorem
określona jest wzorem 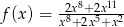 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wtedy liczba
. Wtedy liczba 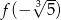 jest równa
jest równa
A) 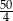 B)
B) 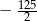 C)
C) 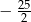 D)
D) 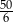
Ciąg 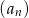 jest określony wzorem
jest określony wzorem 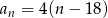 dla
dla 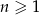 . Suma dziesięciu początkowych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych wyrazów tego ciągu jest równa
A) 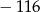 B)
B) 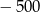 C)
C) 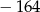 D)
D) 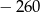
Wartość wyrażenia 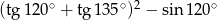 jest równa
jest równa
A) 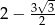 B)
B) 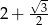 C)
C) 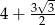 D)
D) 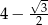
Kąt rozwarcia stożka ma miarę 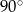 , a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy
A) 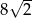 B) 4 C)
B) 4 C) 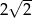 D)
D) 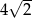
Przekątna równoległoboku dzieli go na dwa trójkąty równoramienne (zobacz rysunek).
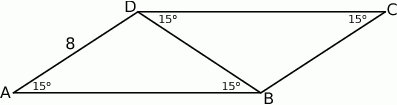
Pole tego równoległoboku jest równe
A) 16 B) 32 C) 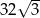 D)
D) 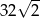
Przedstawione na rysunku trójkąty 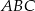 i
i 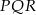 są podobne. Bok
są podobne. Bok 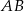 trójkąta
trójkąta 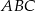 ma długość
ma długość
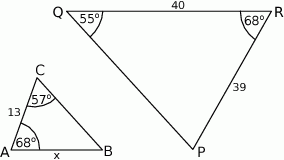
A) 14 B) 16 C) 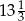 D) 12
D) 12
Gdy przesuniemy wykres funkcji 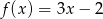 o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
A) 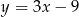 B)
B) 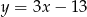 C)
C) 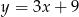 D)
D) 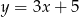
Wśród podanych poniżej nierówności wskaż tę, której zbiorem rozwiązań jest przedział 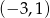 .
.
A) 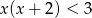 B)
B) 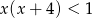 C)
C) 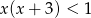 D)
D) 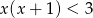
Przekątne deltoidu są zawarte w prostych o równaniach 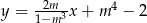 oraz
oraz 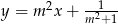 . Zatem
. Zatem
A) 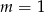 B)
B) 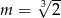 C)
C) 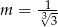 D)
D) 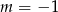
Rzucamy dwa razy sześcienną kostką do gry. Niech 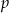 oznacza prawdopodobieństwo tego, że iloczyn liczb otrzymanych oczek dzieli się przez 6. Wtedy
oznacza prawdopodobieństwo tego, że iloczyn liczb otrzymanych oczek dzieli się przez 6. Wtedy
A) 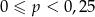 B)
B) 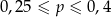 C)
C) 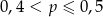 D)
D) 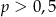
Okręgi o środkach 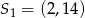 oraz
oraz 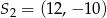 i równych promieniach są styczne zewnętrznie. Promień każdego z tych okręgów jest równy
i równych promieniach są styczne zewnętrznie. Promień każdego z tych okręgów jest równy
A) 26 B) 13 C) 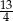 D)
D) 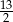
Wszystkich par 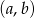 takich, że
takich, że 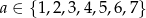 ,
, 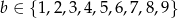 oraz suma
oraz suma 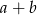 jest podzielna przez 3, jest
jest podzielna przez 3, jest
A) mniej niż 21 B) dokładnie 21 C) dokładnie 22 D) więcej niż 22
Przekątna podstawy ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości ostrosłupa. Ostrosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i środek jednej z krawędzi bocznych (patrz rysunek).
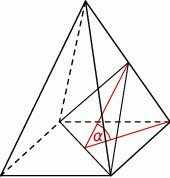
Płaszczyzna przekroju tworzy z podstawą ostrosłupa kąt  o mierze
o mierze
A) 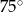 B)
B) 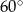 C)
C) 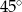 D)
D) 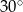
Punkt 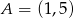 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 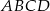 , a punkt
, a punkt 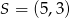 jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A) 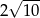 B)
B) 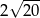 C)
C) 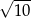 D)
D) 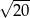
Zadania otwarte
W trapezie 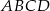 o podstawach
o podstawach 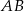 i
i 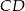 przekątne
przekątne 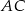 oraz
oraz 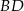 przecinają się w punkcie
przecinają się w punkcie 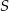 . Wykaż, że jeżeli
. Wykaż, że jeżeli 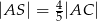 , to pole trójkąta
, to pole trójkąta 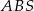 jest 16 razy większe od pola trójkąta
jest 16 razy większe od pola trójkąta 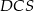 .
.
Rozwiąż równanie 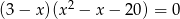 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 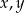 prawdziwa jest nierówność
prawdziwa jest nierówność
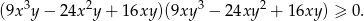
Oblicz prawdopodobieństwo tego, że losowo wybrana liczba trzycyfrowa ma cyfrę setek mniejszą od cyfry dziesiątek, a cyfrę jedności równą cyfrze setek.
Kąt  jest ostry i
jest ostry i 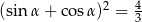 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 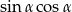 .
.
Poziom natężenia dźwięku w decybelach jest opisany wzorem 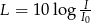 , gdzie
, gdzie 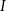 jest natężeniem dźwięku wyrażonym w
jest natężeniem dźwięku wyrażonym w 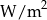 , a
, a 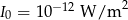 jest stałą nazwaną natężeniem dźwięku odniesienia. Poziom natężenia szeptu wynosi 20 dB, a odpowiadające mu natężenie
jest stałą nazwaną natężeniem dźwięku odniesienia. Poziom natężenia szeptu wynosi 20 dB, a odpowiadające mu natężenie 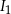 jest 10000 razy mniejsze niż natężenie
jest 10000 razy mniejsze niż natężenie 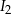 pracującego odkurzacza. Oblicz poziom natężenia dźwięku w decybelach pracującego odkurzacza.
pracującego odkurzacza. Oblicz poziom natężenia dźwięku w decybelach pracującego odkurzacza.
Na rysunku przedstawione są dwa wierzchołki trójkąta prostokątnego 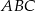 :
: 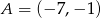 i
i 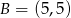 oraz prosta o równaniu
oraz prosta o równaniu 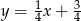 , zawierająca przeciwprostokątną
, zawierająca przeciwprostokątną 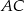 tego trójkąta.
tego trójkąta.
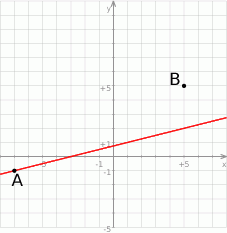
Oblicz współrzędne wierzchołka 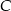 tego trójkąta i długość odcinka
tego trójkąta i długość odcinka 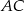 .
.
Dany jest ciąg arytmetyczny 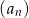 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 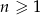 , w którym suma pierwszych 50 wyrazów jest równa 9 900, a suma wyrazów o numerach od 41 do 70 (włącznie) jest równa 540. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
, w którym suma pierwszych 50 wyrazów jest równa 9 900, a suma wyrazów o numerach od 41 do 70 (włącznie) jest równa 540. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 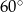 , a krawędź boczna ostrosłupa ma długość
, a krawędź boczna ostrosłupa ma długość 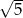 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.

