/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 21 kwietnia 2012 Czas pracy: 170 minut
Zadania zamknięte
Liczba  stanowi 125% liczby
stanowi 125% liczby 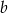 . O ile procent liczba
. O ile procent liczba 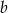 jest mniejsza od liczby
jest mniejsza od liczby  ?
?
A) 25% B) 80% C) 20% D) 120%
Po usunięciu niewymierności z mianownika ułamka 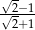 otrzymamy liczbę:
otrzymamy liczbę:
A) 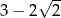 B)
B) 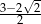 C)
C) 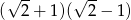 D)
D) 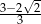
Wskaż rysunek, który może przedstawiać zbiór rozwiązań nierówności 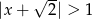 .
.
Do zbioru rozwiązań nierówności 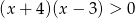 należy liczba
należy liczba
A) 7 B) 3 C) 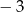 D) 1
D) 1
Rozwiązanie równania 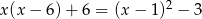 należy do przedziału
należy do przedziału
A) 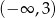 B)
B) 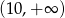 C)
C) 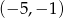 D)
D) 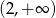
Funkcja liniowa określona wzorem 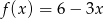 przyjmuje wartości ujemne dla:
przyjmuje wartości ujemne dla:
A) 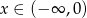 B)
B) 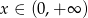 C)
C) 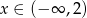 D)
D) 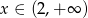
Dla pewnych liczb  i
i 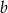 zachodzą równości:
zachodzą równości: 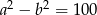 i
i 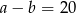 . Dla tych liczb
. Dla tych liczb  i
i 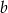 wartość wyrażenia
wartość wyrażenia 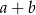 jest równa
jest równa
A) 80 B) 5 C) 10 D) 2
Wyrażenie 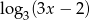 jest określone dla wszystkich liczb
jest określone dla wszystkich liczb  spełniających warunek
spełniających warunek
A) 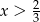 B)
B) 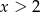 C)
C) 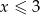 D)
D) 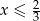
Dane są funkcje 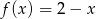 oraz
oraz 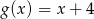 określone dla wszystkich liczb rzeczywistych
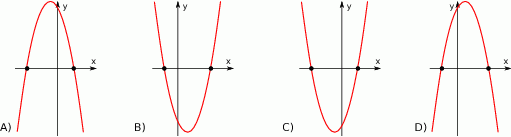
określone dla wszystkich liczb rzeczywistych  . Wskaż, który z poniższych wykresów jest wykresem funkcji
. Wskaż, który z poniższych wykresów jest wykresem funkcji 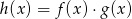 .
.
Nieskończony ciąg liczbowy 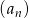 , w którym
, w którym
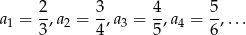
może być opisany wzorem:
A) 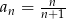 B)
B) 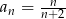 C)
C) 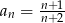 D)
D) 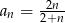
Dane są wielomiany 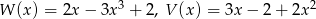 . Stopień wielomianu
. Stopień wielomianu 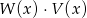 jest równy
jest równy
A) 6 B) 4 C) 5 D) 3
Dany jest nieskończony rosnący ciąg arytmetyczny 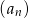 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 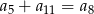 B)
B) 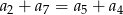 C)
C) 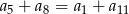 D)
D) 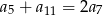
Okrąg opisany na kwadracie ma promień 6. Długość boku tego kwadratu jest równa
A) 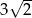 B)
B) 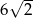 C) 12 D) 6
C) 12 D) 6
Wartość wyrażenia 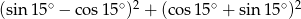 jest równa
jest równa
A) 1 B) 2 C) 0 D) 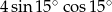
Kąt  jest ostry oraz
jest ostry oraz 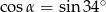 . Wtedy miara kąta
. Wtedy miara kąta  jest równa:
jest równa:
A) 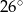 B)
B) 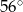 C)
C) 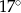 D)
D) 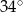
Która z podanych prostych jest styczna do okręgu 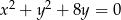 ?
?
A)  B)
B) 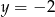 C)
C) 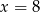 D)
D) 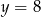
Liczba przekątnych sześcianu to
A) 6 B) 12 C) 8 D) 4
Przekrój osiowy walca jest kwadratem o boku 10. Objętość tego walca jest równa
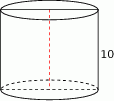
A) 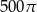 B)
B) 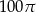 C)
C) 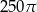 D)
D) 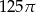
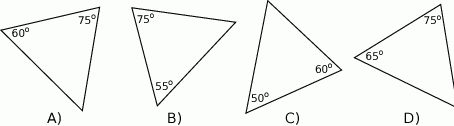
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 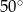 i
i 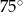 ?
?
W trójkącie prostokątnym o przyprostokątnych długości 6 i 8 połączono wierzchołek  kąta prostego ze środkiem
kąta prostego ze środkiem 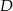 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 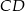 jest równa
jest równa
A) 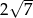 B) 10 C) 7 D) 5
B) 10 C) 7 D) 5
Punkt 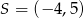 jest środkiem odcinka
jest środkiem odcinka 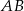 i
i 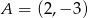 . Punkt
. Punkt 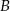 ma współrzędne
ma współrzędne
A) 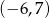 B)
B) 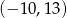 C)
C) 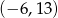 D)
D) 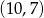
Zadania otwarte
Rozwiąż nierówność 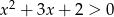 .
.
Ze zbioru 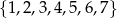 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 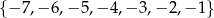 liczbę
liczbę 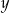 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 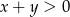 .
.
Rozwiąż równanie 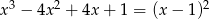 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 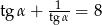 oblicz
oblicz 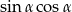 .
.
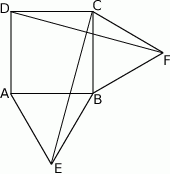
Na zewnątrz kwadratu 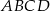 na bokach
na bokach 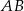 i
i 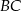 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 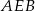 i
i 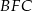 . Uzasadnij, że proste
. Uzasadnij, że proste 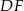 i
i 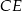 są prostopadłe.
są prostopadłe.
Suma  początkowych wyrazów ciągu geometrycznego
początkowych wyrazów ciągu geometrycznego 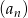 wyraża się wzorem
wyraża się wzorem 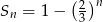 dla
dla 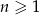 . Oblicz pierwszy wyraz ciągu i jego iloraz.
. Oblicz pierwszy wyraz ciągu i jego iloraz.
Wykaż, że jeśli 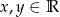 to
to 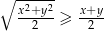 .
.
Punkty 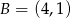 i
i 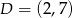 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 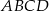 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej  tego rombu.
tego rombu.
W dwóch silosach zbożowych znajdowało się łącznie 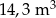 zboża. W ciągu dwóch tygodni zwiększono ilość zboża w pierwszym silosie o 28%, a w drugim o 60%. Po tej zmianie ilość zboża w pierwszym silosie jest dwa razy mniejsza od ilości zboża w drugim silosie. Ile metrów sześciennych zboża znajdowało się początkowo w każdym z silosów?
zboża. W ciągu dwóch tygodni zwiększono ilość zboża w pierwszym silosie o 28%, a w drugim o 60%. Po tej zmianie ilość zboża w pierwszym silosie jest dwa razy mniejsza od ilości zboża w drugim silosie. Ile metrów sześciennych zboża znajdowało się początkowo w każdym z silosów?
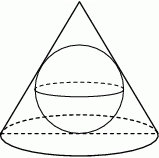
W stożek o wysokości 10 wpisano kulę o promieniu 4. Oblicz pole powierzchni całkowitej stożka.