/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom podstawowy grupa I
2 czerwca 2016 Czas pracy: 170 minut
Zadania zamknięte
Liczba 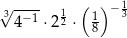 jest równa:
jest równa:
A) 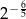 B)
B) 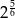 C)
C) 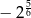 D)
D) 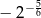
Wykresem funkcji kwadratowej 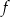 jest parabola o wierzchołku
jest parabola o wierzchołku 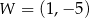 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 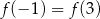 B)
B) 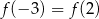 C)
C) 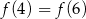 D)
D) 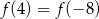
Iloczyn liczby 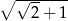 i odwrotności liczby
i odwrotności liczby 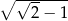 jest równy
jest równy
A) 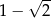 B)
B) 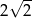 C)
C) 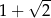 D) 1
D) 1
Na lokacie złożono 1000 zł przy rocznej stopie procentowej 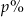 (procent składany). Odsetki naliczane są co kwartał. Po upływie roku wielkość kapitału na lokacie będzie równa
(procent składany). Odsetki naliczane są co kwartał. Po upływie roku wielkość kapitału na lokacie będzie równa
A) 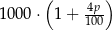 B)
B) 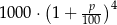 C)
C) 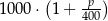 D)
D) 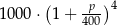
Liczba 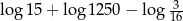 jest równa
jest równa
A) 6 B) 4 C) 5 D) 7
Punkt 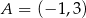 należy do wykresu funkcji
należy do wykresu funkcji 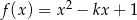 . Zatem
. Zatem 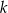 jest równe
jest równe
A) 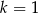 B)
B) 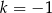 C)
C) 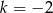 D)
D) 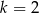
Wartość wyrażenia 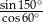 jest równa
jest równa
A) 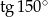 B)
B) 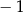 C) 1 D)
C) 1 D) 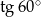
Prosta 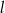 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 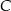 . Jeżeli kąt
. Jeżeli kąt 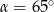 , to miara kąta
, to miara kąta 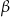 jest równa
jest równa
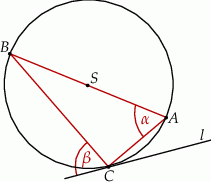
A) 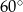 B)
B) 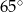 C)
C) 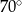 D)
D) 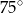
Środek okręgu o promieniu 10 jest oddalony od cięciwy 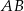 tego okręgu o 6. Długość tej cięciwy jest równa
tego okręgu o 6. Długość tej cięciwy jest równa
A) 10 B) 12 C) 14 D) 16
Dziedziną funkcji 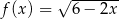 jest przedział
jest przedział
A) 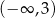 B)
B) 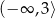 C)
C) 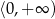 D)
D) 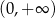
W trójkącie prostokątnym długości przyprostokątnych wynoszą 6 i 8. Stosunek długości odcinków, na które wysokość podzieliła przeciwprostokątną wynosi
A) 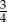 B)
B) 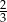 C)
C) 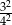 D)
D) 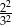
Jeżeli 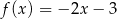 i
i 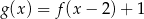 , to funkcja
, to funkcja 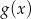 jest równa
jest równa
A) 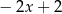 B)
B) 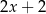 C)
C) 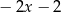 D)
D) 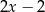
Zbiorem rozwiązań nierówności 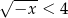 jest przedział
jest przedział
A) 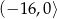 B)
B) 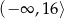 C)
C) 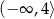 D)
D) 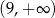
Punkt 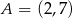 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 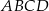 , a punkt
, a punkt 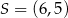 jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A) 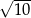 B)
B) 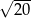 C)
C) 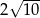 D)
D) 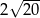
Funkcja 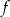 przyporządkowuje każdej liczbie naturalnej resztę z dzielenia tej liczby przez 5. Wówczas
przyporządkowuje każdej liczbie naturalnej resztę z dzielenia tej liczby przez 5. Wówczas 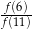 równa się
równa się
A) 1 B) 2 C) 3 D) 4
Na rysunku przedstawiono parabolę, która jest wykresem funkcji 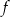 .
.
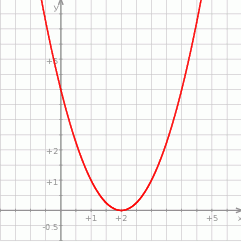
Funkcja f jest określona wzorem
A) 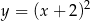 B)
B) 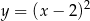 C)
C) 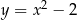 D)
D) 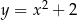
Funkcja 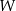 jest określona wzorem
jest określona wzorem 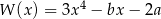 dla wszystkich liczb rzeczywistych. Równość
dla wszystkich liczb rzeczywistych. Równość 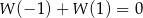 zachodzi, gdy
zachodzi, gdy
A) 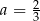 B)
B) 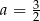 C)
C) 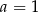 D)
D) 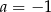
Ciąg 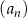 określony dla
określony dla 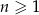 jest arytmetyczny oraz
jest arytmetyczny oraz 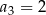 i
i 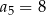 . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A) 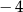 B)
B) 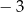 C)
C) 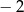 D)
D) 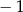
Kąt  jest ostry i
jest ostry i 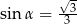 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 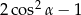 jest równa
jest równa
A) 0 B) 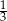 C)
C) 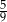 D) 1
D) 1
W ciągu arytmetycznym 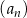 dla
dla 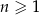 ,
, 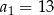 oraz
oraz 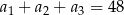 . Wtedy suma
. Wtedy suma 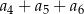 jest równa
jest równa
A) 48 B) 96 C) 75 D) 58
Jeśli 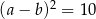 oraz
oraz 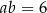 , to
, to 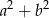 jest równe
jest równe
A) 18 B) 22 C) 20 D) 16
W trójkącie prostokątnym dwa dłuższe boki mają długości 10 i 11. Pole tego trójkąta jest równe
A) 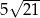 B)
B) 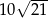 C) 55 D) 110
C) 55 D) 110
Piąty wyraz rosnącego ciągu geometrycznego jest równy 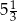 , a siódmy
, a siódmy 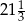 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 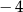 B) 2 C)
B) 2 C) 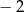 D) 4
D) 4
Odległość między środkami stycznych wewnętrznie okręgów o promieniach  i
i 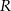 jest równa 7. Odległość między środkami stycznych zewnętrznie okręgów o promieniach
jest równa 7. Odległość między środkami stycznych zewnętrznie okręgów o promieniach  i
i 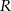 jest równa 23. Promienie
jest równa 23. Promienie  i
i 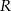 mają długości
mają długości
A) 6 i 17 B) 11 i 12 C) 10 i 13 D) 8 i 15
Prosta o równaniu 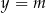 ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej
ma dokładnie jeden punkt wspólny z wykresem funkcji kwadratowej 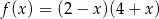 dla
dla
A) 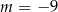 B)
B) 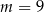 C)
C) 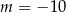 D)
D) 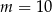
Zadania otwarte
Wyznacz zbiór nieujemnych rozwiązań nierówności 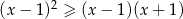 .
.
Różnica między długością przekątnej kwadratu i długością jego boku wynosi 1 cm. Oblicz długość boku tego kwadratu.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 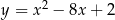 w przedziale
w przedziale 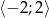 .
.
Wykaż, że stosunek pola kwadratu wpisanego w koło do pola tego koła jest mniejszy od 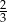 .
.
Wysokości równoległoboku o obwodzie 20 cm mają długości 2 cm i 3 cm. Oblicz pole równoległoboku.
Wykaż, ze dla dowolnych liczb rzeczywistych 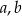 prawdziwa jest nierówność
prawdziwa jest nierówność 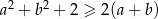 .
.
Wyznacz wzór ogólny funkcji kwadratowej, której największą wartością jest 2, a miejscami zerowymi są liczby 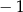 i 3.
i 3.
Trzy liczby dodatnie tworzą ciąg arytmetyczny. Średnia arytmetyczna tych liczb jest równa 10. Jeśli od pierwszej odejmiemy 2, drugą pozostawimy bez zmian, a do trzeciej dodamy 7, to otrzymamy ciąg geometryczny. Wyznacz te liczby.
W trapezie o podstawach długości 10 cm i 6 cm oraz wysokości równej 4 cm poprowadzono przekątne, które podzieliły go na cztery trójkąty. Oblicz pole każdego z otrzymanych trójkątów.

