/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 19 marca 2011 Czas pracy: 180 minut
Przez środek okręgu wpisanego w trójkąt równoboczny 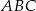 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 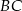 i przecinającą bok
i przecinającą bok 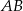 w punkcie
w punkcie 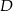 . Oblicz iloraz
. Oblicz iloraz 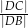 .
.
Dana jest funkcja 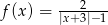 .
.
- Naszkicuj wykres funkcji
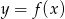 i na jego podstawie wyznacz liczbę rozwiązań równania
i na jego podstawie wyznacz liczbę rozwiązań równania 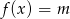 w zależności od parametru
w zależności od parametru 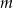 .
. - Liczby
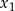 i
i 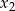 są różnymi pierwiastkami równania
są różnymi pierwiastkami równania 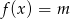 . Oblicz
. Oblicz 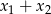 .
.
Między liczby 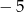 i 49 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
i 49 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
Wierzchołki 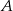 i
i 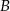 kwadratu
kwadratu 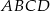 leżą na paraboli
leżą na paraboli 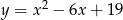 , przy czym odcinek
, przy czym odcinek 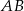 jest równoległy do osi
jest równoległy do osi 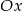 . Wykaż, że jeżeli odległość punktu
. Wykaż, że jeżeli odległość punktu 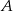 od osi
od osi 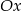 jest liczbą całkowitą to pole kwadratu
jest liczbą całkowitą to pole kwadratu 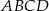 również jest liczbą całkowitą.
również jest liczbą całkowitą.
Okrąg wpisany w trójkąt prostokątny 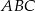 o bokach długości
o bokach długości 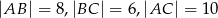 jest styczny do boków
jest styczny do boków 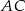 i
i 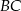 w punktach
w punktach 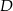 i
i 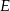 . Proste
. Proste 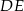 i
i 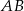 przecinają się punkcie
przecinają się punkcie 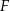 . Oblicz pole trójkąta
. Oblicz pole trójkąta 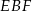 .
.
Dane są punkty 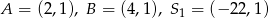 i
i 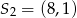 . Odcinek
. Odcinek 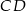 jest obrazem odcinka
jest obrazem odcinka 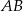 w jednokładności o skali dodatniej i środku
w jednokładności o skali dodatniej i środku 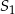 , jak i w jednokładności o skali ujemnej i środku
, jak i w jednokładności o skali ujemnej i środku 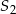 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 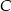 i
i 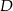 .
.
W nieskończonym ciągu geometrycznym 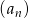 o wyrazach dodatnich każdy wyraz począwszy od trzeciego, jest sumą dwóch poprzednich wyrazów. Oblicz iloraz tego ciągu.
o wyrazach dodatnich każdy wyraz począwszy od trzeciego, jest sumą dwóch poprzednich wyrazów. Oblicz iloraz tego ciągu.
Wielomian 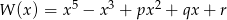 jest podzielny przez wielomian
jest podzielny przez wielomian 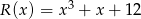 . Wyznacz liczby
. Wyznacz liczby 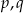 i
i  .
.
Wyznacz wszystkie liczby naturalne  spełniające równanie
spełniające równanie
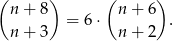
Rzucamy 9 razy symetryczną 6-ścienną kostką do gry. Jakie jest prawdopodobieństwo, że w każdych trzech kolejnych rzutach otrzymamy trzy różne liczby oczek?
Odległość środka podstawy ostrosłupa prawidłowego czworokątnego od krawędzi bocznej równa się  , a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się
, a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się 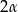 . Oblicz wysokość ostrosłupa.
. Oblicz wysokość ostrosłupa.

