/Szkoła średnia/Zadania maturalne
Dowody w geometrii podobieństwo II
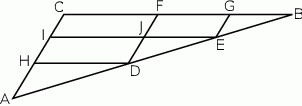
Prosta przechodząca przez wierzchołek 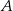 równoległoboku
równoległoboku 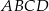 przecina jego przekątną
przecina jego przekątną 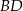 w punkcie
w punkcie 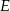 i bok
i bok 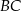 w punkcie
w punkcie 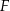 , a prostą
, a prostą 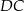 w punkcie
w punkcie 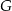 . Udowodnij, że
. Udowodnij, że
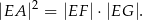
W trapezie 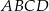 (
(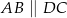 ) przekątne
) przekątne 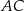 i
i 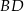 przecinają się w punkcie
przecinają się w punkcie 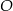 takim, że
takim, że 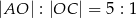 . Pole trójkąta
. Pole trójkąta 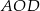 jest równe 10. Uzasadnij, że pole trapezu
jest równe 10. Uzasadnij, że pole trapezu 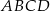 jest równe 72.
jest równe 72.

Na bokach 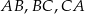 trójkąta równobocznego
trójkąta równobocznego 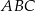 wybrano kolejno punkty
wybrano kolejno punkty 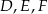 tak, że
tak, że 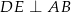 ,
, 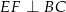 i
i 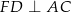 .
.
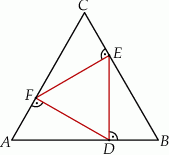
Wykaż, że trójkąt 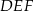 jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta
jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta 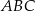 .
.
W trójkącie równobocznym 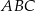 połączono środki wysokości otrzymując trójkąt
połączono środki wysokości otrzymując trójkąt 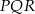 . Wykaż, że stosunek pola trójkąta
. Wykaż, że stosunek pola trójkąta 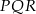 do pola trójkąta
do pola trójkąta 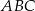 jest równy
jest równy 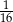 .
.
Na bokach 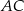 i
i 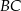 trójkąta
trójkąta 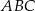 obrano punkty
obrano punkty 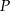 i
i 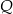 takie, że
takie, że 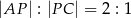 oraz
oraz 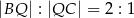 . Odcinki
. Odcinki 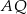 i
i 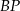 przecinają się w punkcie
przecinają się w punkcie 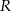 . Wykaż, że pole czworokąta
. Wykaż, że pole czworokąta 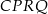 jest równe polu trójkąta
jest równe polu trójkąta 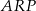 .
.
Odcinki 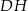 i
i 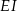 są równoległe do boku
są równoległe do boku 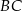 trójkąta
trójkąta 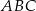 , a odcinki
, a odcinki 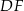 i
i 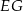 są równoległe do boku
są równoległe do boku 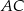 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 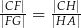 , to
, to 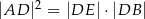 .
.
Dany jest trójkąt 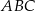 . Na boku
. Na boku 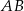 tego trójkąta obrano punkty
tego trójkąta obrano punkty 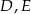 i
i 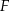 tak, że
tak, że 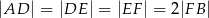 . Na bokach
. Na bokach 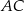 i
i 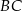 obrano – odpowiednio – punkty
obrano – odpowiednio – punkty 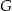 i
i 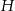 tak, że
tak, że 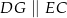 oraz
oraz 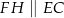 (zobacz rysunek). Wykaż, że jeżeli pole trójkąta
(zobacz rysunek). Wykaż, że jeżeli pole trójkąta 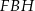 jest równe
jest równe 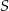 , to pole trójkąta
, to pole trójkąta 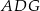 jest równe
jest równe 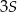 .
.
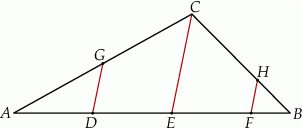
Na bokach 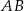 i
i 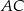 trójkąta
trójkąta 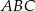 wybrano odpowiednio punkty
wybrano odpowiednio punkty 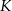 i
i 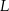 w ten sposób, że
w ten sposób, że 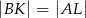 . Punkt
. Punkt 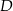 jest środkiem odcinka
jest środkiem odcinka 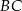 . Przez punkty
. Przez punkty 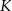 i
i 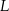 poprowadzono proste równoległe do
poprowadzono proste równoległe do 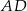 , które wyznaczyły na boku
, które wyznaczyły na boku 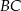 punkty
punkty 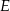 i
i 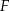 odpowiednio (zobacz rysunek). Wykaż, że jeżeli
odpowiednio (zobacz rysunek). Wykaż, że jeżeli 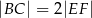 , to
, to 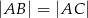 .
.
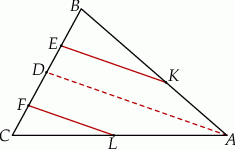
Na ramionach 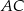 i
i 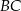 trójkąta równoramiennego
trójkąta równoramiennego 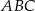 wybrano punkty
wybrano punkty 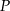 i
i 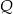 w ten sposób, że odcinek
w ten sposób, że odcinek 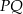 jest równoległy do podstawy
jest równoległy do podstawy 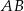 i styczny do okręgu wpisanego w trójkąt
i styczny do okręgu wpisanego w trójkąt 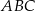 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 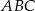 jest równe
jest równe
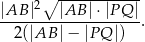
Punkt 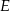 jest środkiem boku
jest środkiem boku 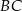 prostokąta
prostokąta 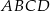 , w którym
, w którym 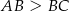 . Punkt
. Punkt 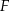 leży na boku
leży na boku 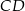 tego prostokąta oraz
tego prostokąta oraz 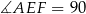 . Udowodnij, że
. Udowodnij, że 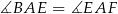 .
.
Przekątne trapezu przecinają się w punkcie 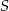 . Przez punkt
. Przez punkt 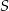 poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach
poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach 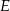 i
i 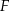 . Wykaż, że
. Wykaż, że 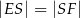 .
.
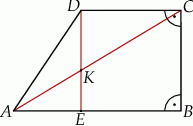
W trapezie prostokątnym 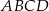 (rysunek) punkt
(rysunek) punkt 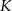 jest punktem przecięcia wysokości
jest punktem przecięcia wysokości 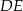 i przekątnej
i przekątnej 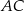 tego trapezu. Wiedząc, że
tego trapezu. Wiedząc, że 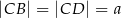 i
i 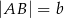 wykaż, że pole
wykaż, że pole 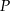 czworokąta
czworokąta 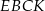 jest równe
jest równe 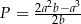 .
.
Dany jest trójkąt równoramienny 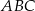 , w którym
, w którym 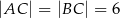 , a punkt
, a punkt 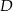 jest środkiem podstawy
jest środkiem podstawy 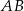 . Okrąg o środku
. Okrąg o środku 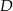 jest styczny do prostej
jest styczny do prostej  w punkcie
w punkcie 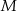 . Punkt
. Punkt 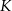 leży na boku
leży na boku 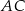 , punkt
, punkt 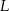 leży na boku
leży na boku 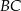 , odcinek
, odcinek 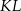 jest styczny do rozważanego okręgu oraz
jest styczny do rozważanego okręgu oraz 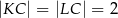 (zobacz rysunek).
(zobacz rysunek).
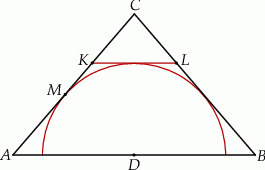
Wykaż, że 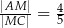 .
.

