/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas trzecich)
poziom rozszerzony 24 stycznia 2013 Czas pracy: 180 minut
Niech  i
i 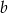 będą długościami kolejnych boków równoległoboku
będą długościami kolejnych boków równoległoboku 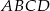 , zaś
, zaś 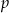 i
i  długościami jego przekątnych. Wykaż, że
długościami jego przekątnych. Wykaż, że 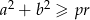 .
.
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 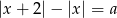 nie ma rozwiązania.
nie ma rozwiązania.
Oblicz wartość wyrażenia 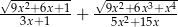 dla
dla 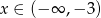 .
.
Wyznacz dziedzinę funkcji 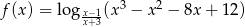 .
.
Rozwiąż układ równań 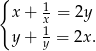
W trójkącie 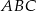 dwa kąty przy wierzchołkach
dwa kąty przy wierzchołkach 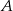 i
i 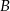 mają odpowiednio miary:
mają odpowiednio miary: 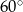 i
i 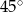 . Oblicz pole tego trójkąta, wiedząc, że długość boku
. Oblicz pole tego trójkąta, wiedząc, że długość boku 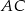 jest równa
jest równa 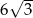 .
.
Znajdź taki punkt 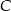 , leżący na prostej
, leżący na prostej 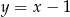 , aby pole trójkąta
, aby pole trójkąta 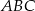 , którego wierzchołkami są punkty:
, którego wierzchołkami są punkty: 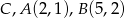 było równe 5.
było równe 5.
Dla jakiego 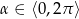 pierwiastki równania
pierwiastki równania
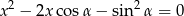
spełniają warunek 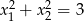 ?
?
Wykaż, że objętość sześcianu jest sześć razy większa od objętości ośmiościanu foremnego, wyznaczonego przez środki ścian tego sześcianu.
Na trzy półki kładziemy losowo 5 książek. Jakie jest prawdopodobieństwo tego, że jedna (i tylko jedna) z półek zostanie pusta?.
Pierwszy wyraz ciągu arytmetycznego 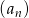 wynosi 1. Dla jakiej wartości różnicy
wynosi 1. Dla jakiej wartości różnicy  wyrażenie
wyrażenie 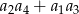 ma wartość najmniejszą i ile ona wynosi?
ma wartość najmniejszą i ile ona wynosi?

