/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy
(technikum) 11 kwietnia 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 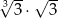 jest równa
jest równa
A) 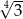 B)
B) 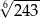 C)
C) 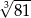 D)
D) 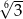
Liczba  stanowi 20% liczby
stanowi 20% liczby 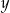 . Zatem prawdziwe jest następujące równanie
. Zatem prawdziwe jest następujące równanie
A) 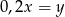 B)
B) 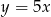 C)
C) 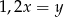 D)
D) 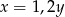
Wartość wyrażenia 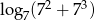 wynosi
wynosi
A) 5 B) 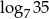 C)
C) 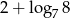 D)
D) 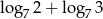
Jeżeli 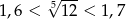 to liczba
to liczba 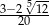 należy do przedziału
należy do przedziału
A) 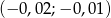 B)
B) 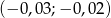 C)
C) 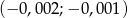 D)
D) 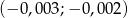
Wskaż rysunek, który może przedstawiać zbiór rozwiązań nierówności 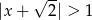 .
.
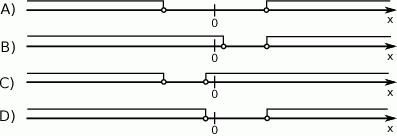
Liczba 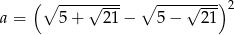 jest równa
jest równa
A) 4 B) 6 C) 10 D) 14
Korzystając z danego wykresu funkcji 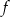 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą
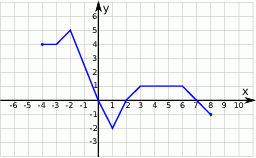
A) 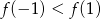 B)
B) 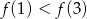 C)
C) 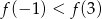 D)
D) 
Prosta o równaniu 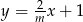 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 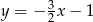 . Stąd wynika, że
. Stąd wynika, że
A) 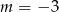 B)
B) 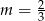 C)
C) 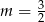 D)
D) 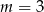
Przybliżenie liczby 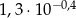 jest równe 0,5175393. Przybliżeniem liczby
jest równe 0,5175393. Przybliżeniem liczby 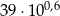 z dokładnością do 3 miejsca po przecinku jest liczba
z dokładnością do 3 miejsca po przecinku jest liczba
A) 15,526 B) 1552,618 C) 155,262 D) 1552,617
Wyrażenie 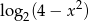 jest określone dla wszystkich liczb
jest określone dla wszystkich liczb  spełniających warunek
spełniających warunek
A) 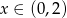 B)
B) 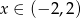 C)
C) 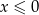 D)
D) 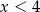
Rozwiązaniem równania 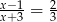 jest liczba
jest liczba
A) 1 B) 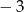 C) 9 D)
C) 9 D) 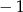
Jeżeli  i
i 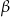 są miarami kątów ostrych trójkąta prostokątnego oraz
są miarami kątów ostrych trójkąta prostokątnego oraz 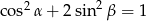 to
to
A) 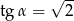 B)
B) 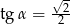 C)
C) 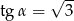 D)
D) 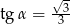
Jeżeli funkcja 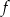 jest określona wzorem
jest określona wzorem 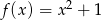 , to funkcję
, to funkcję 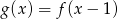 opisuje wzór
opisuje wzór
A) 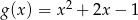
B) 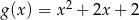
C) 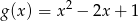
D) 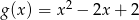
W ciągu arytmetycznym piąty wyraz jest równy 11, a dziewiąty jest równy 25. Różnica tego ciągu jest równa
A) 14 B)  C) 7 D)
C) 7 D) 
Ciąg 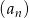 określony jest wzorem
określony jest wzorem 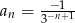 . Piąty wyraz tego ciągu to
. Piąty wyraz tego ciągu to
A) 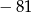 B)
B) 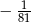 C) 81 D)
C) 81 D) 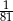
Punkt 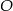 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 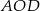 ma miarę
ma miarę
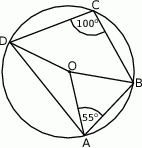
A) 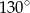 B)
B) 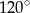 C)
C) 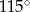 D)
D) 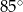
Dany jest nieskończony rosnący ciąg geometryczny 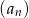 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 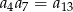 B)
B) 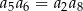 C)
C) 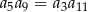 D)
D) 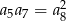
Wybieramy jedną liczbę ze zbioru 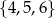 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 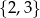 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
A) 6 B) 5 C) 4 D) 3
Pole sześciokąta foremnego o boku długości 6 jest równe
A) 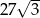 B)
B) 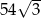 C)
C) 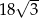 D)
D) 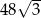
W czterech rzutach sześcienną kostką do gry otrzymano następujące liczby oczek: 6, 3, 1, 2. Mediana tych danych jest równa
A) 2 B) 2,5 C) 3 D) 3,5
Prosta 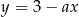 jest równoległa do prostej
jest równoległa do prostej 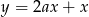 . Wtedy
. Wtedy
A) 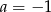 B)
B) 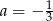 C)
C) 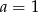 D)
D) 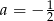
Objętość graniastosłupa prawidłowego trójkątnego o wysokości 7 jest równa 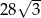 . Długość krawędzi podstawy tego graniastosłupa jest równa
. Długość krawędzi podstawy tego graniastosłupa jest równa
A) 2 B) 4 C) 8 D) 16
Zadania otwarte
Rozwiąż nierówność: 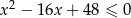 .
.
Ciąg 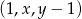 jest arytmetyczny, natomiast ciąg
jest arytmetyczny, natomiast ciąg 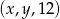 jest geometryczny. Oblicz
jest geometryczny. Oblicz  oraz
oraz 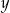 i podaj ten ciąg geometryczny.
i podaj ten ciąg geometryczny.
Uzasadnij, że jeżeli prostokąt 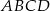 nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.
nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.

Wykaż, że dla dowolnych liczb rzeczywistych 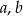 spełniona jest nierówność
spełniona jest nierówność
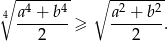
Rozwiąż równanie 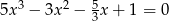 .
.
Oblicz, ile jest liczb naturalnych trzycyfrowych, które są podzielne przez 5, i których zapis składa się z 3 różnych cyfr.
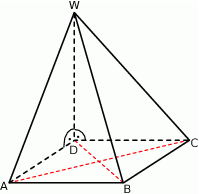
Podstawą ostrosłupa 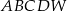 jest kwadrat
jest kwadrat 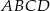 . Krawędź boczna
. Krawędź boczna 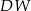 jest wysokością tego ostrosłupa. Krawędzie boczne
jest wysokością tego ostrosłupa. Krawędzie boczne 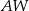 i
i 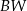 mają następujące długości:
mają następujące długości: 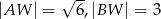 . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
Punkty 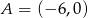 i
i 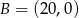 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 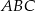 o przeciwprostokątnej
o przeciwprostokątnej 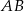 . Wierzchołek
. Wierzchołek 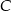 leży na prostej o równaniu
leży na prostej o równaniu 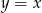 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 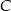 .
.
Dwa miasta łączy linia kolejowa o długości 336 kilometrów. Pierwszy pociąg przebył tę trasę w czasie o 40 minut krótszym niż drugi pociąg. Średnia prędkość pierwszego pociągu na tej trasie była o 9 km/h większa od średniej prędkości drugiego pociągu. Oblicz średnią prędkość każdego z tych pociągów na tej trasie.

