/Szkoła średnia/Zadania maturalne
Poprawkowy Egzamin Maturalny
z Matematyki poziom podstawowy 8 września 2020 Czas pracy: 170 minut
Zadania zamknięte
Liczba 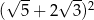 jest równa
jest równa
A) 11 B) 17 C) 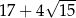 D)
D) 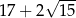
Liczbę 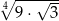 można zapisać w postaci
można zapisać w postaci
A) 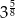 B)
B) 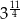 C)
C) 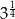 D)
D) 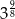
Liczba 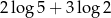 jest równa
jest równa
A) 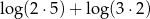 B)
B) 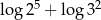
C) 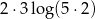 D)
D) 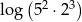
Najmniejszą liczbą całkowitą spełniającą nierówność 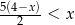 jest liczba
jest liczba
A) 1 B) 2 C) 3 D) 4
W zestawie 250 liczb występują jedynie liczby 4 i 2. Liczba 4 występuje 128 razy, a liczba 2 występuje 122 razy. Przyjęto przybliżenie średniej arytmetycznej zestawu tych wszystkich liczb do liczby 3. Błąd bezwzględny tego przybliżenia jest równy
A) 0,024 B) 0,24 C) 0,0024 D) 0,00024
Na początku miesiąca komputer kosztował 3 500 zł. W drugiej dekadzie tego miesiąca cenę komputera obniżono o 10%, a w trzeciej dekadzie cena tego komputera została jeszcze raz obniżona, tym razem o 15%. Innych zmian ceny tego komputera w tym miesiącu już nie było. Cena komputera na koniec miesiąca była równa
A) 3 272,50 zł B) 2 625 zł C) 2 677,50 zł D) 2 800 zł
Funkcje liniowe 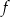 i
i 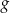 określone wzorami
określone wzorami 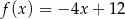 i
i 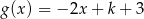 mają wspólne miejsce zerowe. Stąd wynika, że
mają wspólne miejsce zerowe. Stąd wynika, że
A) 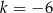 B)
B) 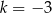 C)
C) 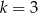 D)
D) 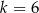
Zbiorem wartości funkcji kwadratowej 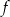 określonej wzorem
określonej wzorem 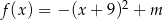 jest przedział
jest przedział 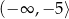 . Wtedy
. Wtedy
A) 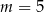 B)
B) 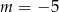 C)
C) 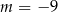 D)
D) 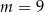
Osią symetrii wykresu funkcji kwadratowej 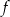 określonej wzorem
określonej wzorem 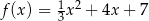 jest prosta o równaniu
jest prosta o równaniu
A) 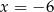 B)
B) 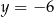 C)
C) 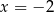 D)
D) 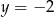
Na rysunku poniżej przedstawiono fragment wykresu funkcji kwadratowej 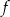 określonej wzorem
określonej wzorem 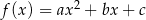 .
.
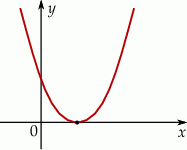
Stąd wynika, że:
A) 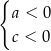 B)
B) 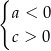 C)
C) 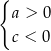 D)
D) 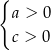
Rozwiązaniem równania 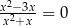 jest liczba
jest liczba
A) 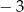 B) 0 C) 3 D) 9
B) 0 C) 3 D) 9
Do okręgu o środku w punkcie 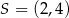 należy punkt
należy punkt 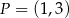 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 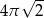 B)
B) 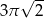 C)
C) 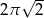 D)
D) 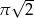
Prosta 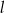 jest równoległa do prostej
jest równoległa do prostej 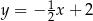 . Na prostej
. Na prostej 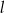 leży punkt
leży punkt 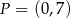 . Zatem równanie prostej
. Zatem równanie prostej 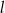 ma postać
ma postać
A) 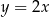 B)
B) 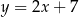 C)
C) 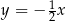 D)
D) 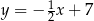
Punkt 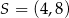 jest środkiem odcinka
jest środkiem odcinka 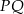 , którego koniec
, którego koniec 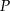 leży na osi
leży na osi 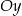 , a koniec
, a koniec 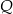 – na osi
– na osi 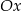 . Wynika stąd, że
. Wynika stąd, że
A) 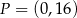 i
i 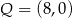 B)
B) 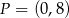 i
i 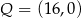
C) 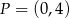 i
i 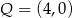 D)
D) 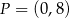 i
i 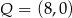
Przyprostokątna 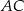 trójkąta prostokątnego
trójkąta prostokątnego 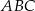 ma długość 6, a wysokość
ma długość 6, a wysokość 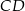 dzieli go na dwa takie trójkąty
dzieli go na dwa takie trójkąty 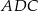 i
i 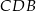 , że pole trójkąta
, że pole trójkąta 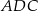 jest 4 razy większe od pola trójkąta
jest 4 razy większe od pola trójkąta 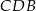 (zobacz rysunek).
(zobacz rysunek).
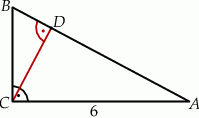
Przyprostokątna 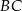 trójkąta prostokątnego
trójkąta prostokątnego 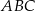 jest równa
jest równa
A) 1,5 B) 2 C) 2,5 D) 3
Punkty 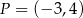 i
i 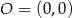 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem nachylenia tej prostej do osi
jest kątem nachylenia tej prostej do osi 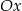 (zobacz rysunek).
(zobacz rysunek).
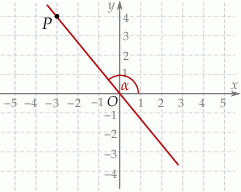
Wtedy tangens kąta  jest równy
jest równy
A) 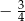 B)
B) 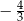 C)
C) 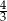 D)
D) 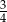
Kąt  jest ostry oraz
jest ostry oraz 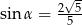 . Wtedy
. Wtedy
A) 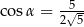 B)
B) 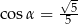 C)
C) 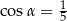 D)
D) 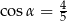
W ciągu arytmetycznym 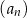 , określonym dla każdej liczby naturalnej
, określonym dla każdej liczby naturalnej 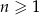 , są dane dwa wyrazy:
, są dane dwa wyrazy: 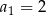 i
i 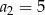 . Stąd wynika, że
. Stąd wynika, że  –ty wyraz tego ciągu jest określony wzorem
–ty wyraz tego ciągu jest określony wzorem
A) 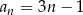 B)
B) 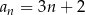 C)
C) 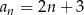 D)
D) 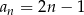
Funkcja 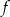 jest określona wzorem
jest określona wzorem 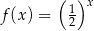 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych  . Funkcja
. Funkcja 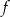 dla argumentu
dla argumentu 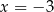 przyjmuje wartość
przyjmuje wartość
A)  B)
B)  C) 6 D) 8
C) 6 D) 8
Wielkości  i
i 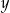 są odwrotnie proporcjonalne (tabela poniżej).
są odwrotnie proporcjonalne (tabela poniżej).
 |  | 3 | 8 |
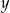 | 36 | 24 | 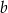 |
Stąd wynika, że
A) 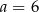 ,
, 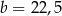 B)
B) 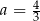 ,
, 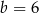 C)
C) 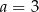 ,
, 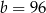 D)
D) 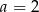 ,
, 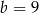
W prostokątnym układzie współrzędnych na płaszczyźnie parę prostych prostopadłych opisują równania
A) 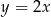 i
i 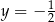 B)
B) 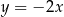 i
i 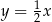
C) 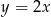 i
i 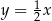 D)
D) 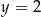 i
i 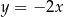
Dane są punkty 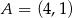 ,
, 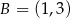 ,
, 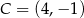 . Pole trójkąta
. Pole trójkąta 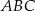 jest równe
jest równe
A) 3 B) 6 C) 8 D) 16
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2020 i podzielnych przez 4?
A) 506 B) 505 C) 256 D) 255
Dane są graniastosłup i ostrosłup o takich samych podstawach. Liczba wszystkich wierzchołków tego graniastosłupa jest o 9 większa od liczby wszystkich wierzchołków tego ostrosłupa. Podstawą każdej z tych brył jest
A) dziewięciokąt. B) ośmiokąt. C) osiemnastokąt. D) dziesięciokąt.
Pole powierzchni całkowitej sześcianu jest równe 12. Suma długości wszystkich krawędzi tego sześcianu jest równa
A) 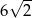 B)
B) 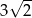 C)
C) 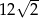 D)
D) 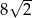
Zadania otwarte
Rozwiąż nierówność: 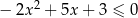 .
.
Dany jest trzywyrazowy ciąg 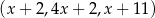 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Wykaż, że dla dowolnych różnych liczb rzeczywistych  i
i 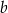 prawdziwa jest nierówność
prawdziwa jest nierówność
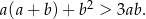
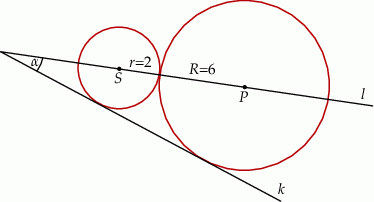
Dwa okręgi o promieniach 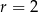 i
i 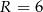 są styczne zewnętrznie i są styczne do wspólnej prostej
są styczne zewnętrznie i są styczne do wspólnej prostej 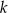 . Wykaż, że prosta
. Wykaż, że prosta 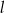 przechodząca przez środki
przechodząca przez środki 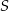 i
i 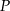 tych okręgów przecina prostą
tych okręgów przecina prostą 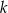 pod kątem
pod kątem 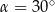 (zobacz rysunek).
(zobacz rysunek).
Rozwiąż równanie 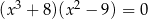 .
.
W pudełku jest 8 kul, z czego 5 białych i 3 czarne. Do tego pudełka dołożono  kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe
kul białych. Doświadczenie polega na losowaniu jednej kuli z tego pudełka. Prawdopodobieństwo, że będzie to kula biała, jest równe 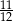 . Oblicz
. Oblicz  .
.
Dany jest trójkąt równoramienny 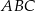 , w którym podstawa
, w którym podstawa 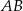 ma długość 12, a każde z ramion
ma długość 12, a każde z ramion 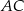 i
i 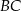 ma długość równą 10. Punkt
ma długość równą 10. Punkt 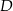 jest środkiem ramienia
jest środkiem ramienia 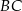 (zobacz rysunek).
(zobacz rysunek).
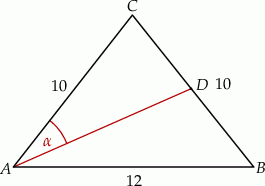
Oblicz sinus kąta  , jaki środkowa
, jaki środkowa 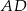 tworzy z ramieniem
tworzy z ramieniem 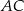 trójkąta
trójkąta 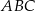 .
.
Pole powierzchni bocznej stożka jest trzy razy większe od pola jego podstawy. Wysokość tego stożka jest równa 12. Oblicz objętość tego stożka.
Prosta o równaniu 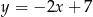 jest symetralną odcinka
jest symetralną odcinka 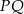 , gdzie
, gdzie 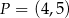 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 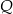 .
.

