/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 1 maja 2021 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 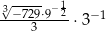 jest równa
jest równa
A) 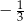 B)
B) 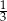 C) 1 D)
C) 1 D) 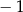
Dane są liczby 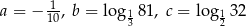 . Iloczyn
. Iloczyn 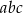 jest równy
jest równy
A) 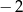 B)
B) 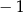 C)
C) 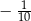 D)
D) 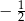
Koszt brutto wysłania SMS-a w usłudze Premium SMS wynosi 17,22 zł. Jaka jest wartość netto tego SMS-a, jeżeli koszt SMS-a obciążony jest 19% podatkiem dochodowym oraz 23% podatkiem VAT?
A) 7,12 zł B) 10,74 zł C) 25,20 zł D) 11,76 zł
Równość 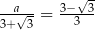 zachodzi dla
zachodzi dla
A) 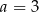 B)
B) 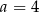 C)
C) 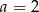 D)
D) 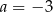
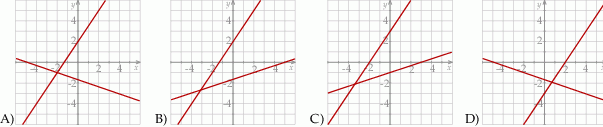
Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań 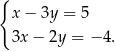 Wskaż ten rysunek:
Wskaż ten rysunek:
Liczba niewymiernych rozwiązań równania 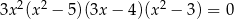 jest równa
jest równa
A) 1 B) 2 C) 4 D) 5
Ile liczb całkowitych  spełnia nierówność
spełnia nierówność 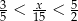 ?
?
A) 27 B) 28 C) 29 D) 30
Funkcja 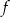 jest określona wzorem
jest określona wzorem 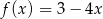 dla każdej liczby z przedziału
dla każdej liczby z przedziału 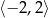 . Zbiorem wartości tej funkcji jest przedział
. Zbiorem wartości tej funkcji jest przedział
A) 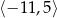 B)
B) 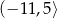 C)
C) 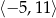 D)
D) 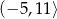
Na rysunku przedstawiono wykres funkcji 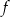 .
.
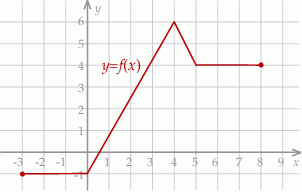
Funkcja 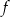 jest malejąca w przedziale
jest malejąca w przedziale
A) 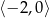 B)
B) 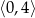 C)
C) 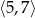 D)
D) 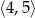
Funkcja 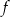 jest określona wzorem
jest określona wzorem 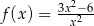 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 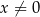 . Wówczas wartość funkcji
. Wówczas wartość funkcji 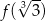 jest równa
jest równa
A) 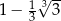 B)
B) 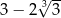 C)
C) 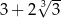 D)
D) 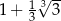
Ciąg geometryczny 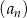 jest określony wzorem
jest określony wzorem 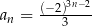 dla
dla 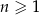 . Suma jedenastu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma jedenastu początkowych kolejnych wyrazów tego ciągu jest równa
A) 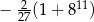 B)
B) 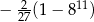 C)
C) 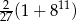 D)
D) 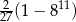
Suma kwadratów czterech początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie 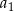 i różnicy
i różnicy  wyraża się wzorem
wyraża się wzorem
A) 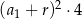 B)
B) 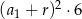 C)
C) 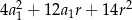 D)
D) 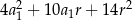
Odcinek 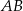 jest średnicą okręgu o środku
jest średnicą okręgu o środku 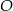 .
.
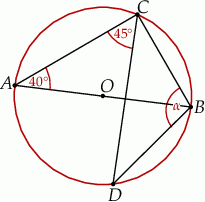
Miara kąta 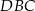 oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa
A) 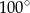 B)
B) 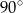 C)
C) 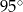 D)
D) 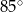
Ciąg liczbowy określony jest wzorem 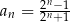 , dla
, dla 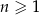 . Szósty wyraz tego ciągu jest równy
. Szósty wyraz tego ciągu jest równy
A) 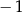 B)
B) 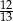 C)
C) 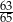 D) 1
D) 1
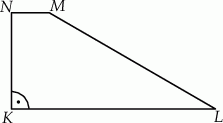
W trapezie 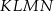 , w którym
, w którym 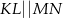 , kąt
, kąt 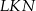 jest prosty (zobacz rysunek) oraz dane są:
jest prosty (zobacz rysunek) oraz dane są: 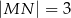 ,
, 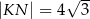 ,
, 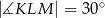 . Pole tego trapezu jest równe:
. Pole tego trapezu jest równe:
A) 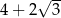 B)
B) 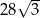 C)
C) 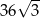 D)
D) 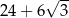
Liczby 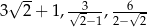 są kolejnymi wyrazami ciągu
są kolejnymi wyrazami ciągu
A) arytmetycznego B) geometrycznego C) rosnącego D) malejącego
W kwadracie 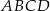 połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat 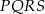 .
.
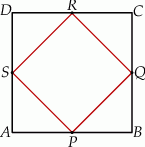
Kwadrat 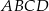 jest podobny do kwadratu
jest podobny do kwadratu 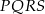 w skali
w skali
A) 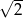 B) 2 C)
B) 2 C) 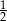 D)
D) 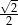
Punkt 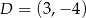 jest obrazem punktu
jest obrazem punktu 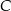 w symetrii względem punktu
w symetrii względem punktu 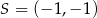 , a punkt
, a punkt 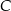 jest środkiem odcinka
jest środkiem odcinka 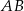 , gdzie
, gdzie 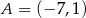 . Punkt
. Punkt 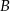 ma współrzędne
ma współrzędne
A) 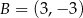 B)
B) 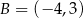 C)
C) 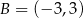 D)
D) 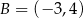
Jeżeli 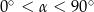 oraz
oraz 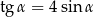 , to
, to
A) 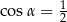 B)
B) 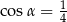 C)
C) 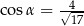 D)
D) 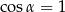
Współczynnik kierunkowy prostej, na której leżą punkty 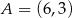 oraz
oraz 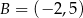 , jest równy
, jest równy
A) 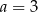 B)
B) 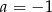 C)
C) 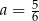 D)
D) 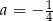
Prosta 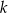 przecina oś
przecina oś 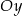 układu współrzędnych w punkcie
układu współrzędnych w punkcie 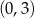 i jest prostopadła do prostej o równaniu
i jest prostopadła do prostej o równaniu 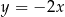 . Wówczas prosta
. Wówczas prosta 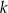 przecina oś
przecina oś 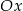 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 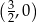 B)
B) 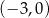 C)
C) 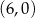 D)
D) 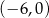
Prosta 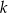 przecina oś
przecina oś 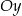 układu współrzędnych w punkcie
układu współrzędnych w punkcie 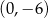 i jest równoległa do prostej o równaniu
i jest równoległa do prostej o równaniu 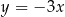 . Wówczas prosta
. Wówczas prosta 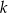 przecina oś
przecina oś 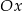 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 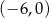 B)
B) 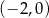 C)
C) 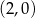 D)
D) 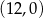
W trójkącie 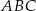 , w którym
, w którym 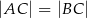 , na boku
, na boku 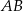 wybrano punkt
wybrano punkt 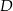 taki, że
taki, że 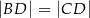 oraz
oraz 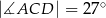 (zobacz rysunek).
(zobacz rysunek).
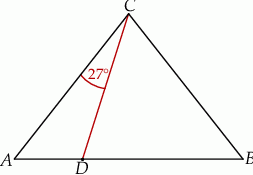
Wynika stąd, że kąt 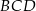 ma miarę
ma miarę
A) 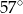 B)
B) 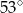 C)
C) 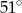 D)
D) 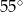
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 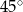 , a wysokość ostrosłupa jest równa 6. Wysokość podstawy tego ostrosłupa ma długość
, a wysokość ostrosłupa jest równa 6. Wysokość podstawy tego ostrosłupa ma długość
A) 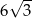 B) 9 C) 12 D)
B) 9 C) 12 D) 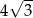
Na loterię przygotowano pulę 200 losów, w tym 4 wygrywające. Po wylosowaniu pewnej liczby losów, wśród których były dokładnie dwa wygrywające, szansa na wygraną była taka sama jak przed rozpoczęciem loterii. Stąd wynika, że wylosowano
A) 8 losów. B) 40 losów. C) 100 losów. D) 50 losów.
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 6 i niepodzielnych przez 9?
A) 60 B) 120 C) 100 D) 150
W pewnej loterii fantowej przygotowano dwie urny z losami, przy czym w drugiej urnie było trzy razy więcej losów niż w pierwszej urnie. Prawdopodobieństwo wybrania losu wygrywającego z pierwszej urny jest równe  , a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe
, a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe 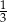 . Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
. Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
A) 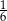 B)
B) 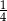 C)
C) 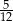 D)
D) 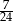
Średnia arytmetyczna zestawu danych: 7, 12, 8, 6,  ,
, 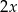 jest taka sama jak średnia arytmetyczna zestawu danych: 11, 8, 9, 3,
jest taka sama jak średnia arytmetyczna zestawu danych: 11, 8, 9, 3,  ,
,  ,
, 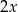 . Wynika stąd, że
. Wynika stąd, że
A) 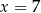 B)
B) 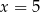 C)
C) 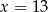 D)
D) 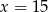
Zadania otwarte
Wyznacz wszystkie liczby dodatnie  spełniające nierówność
spełniające nierówność 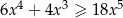 .
.
Rozwiąż równanie 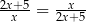 , gdzie
, gdzie 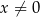 i
i 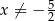 .
.
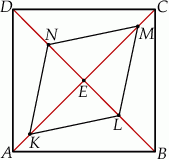
Dany jest kwadrat 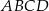 . Przekątne
. Przekątne 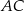 i
i 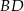 przecinają się w punkcie
przecinają się w punkcie 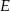 . Punkty
. Punkty 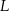 i
i 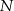 są środkami odcinków – odpowiednio –
są środkami odcinków – odpowiednio – 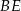 i
i 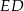 . Punkty
. Punkty 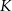 i
i 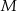 leżą na przekątnej
leżą na przekątnej 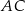 tak, że
tak, że 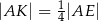 i
i 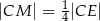 (zobacz rysunek). Wykaż, że stosunek pola czworokąta
(zobacz rysunek). Wykaż, że stosunek pola czworokąta 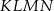 do pola kwadratu
do pola kwadratu 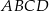 jest równy 3:8.
jest równy 3:8.
Wiedząc, że 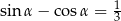 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 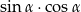 .
.
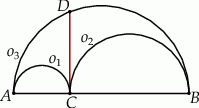
Na średnicy 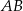 półokręgu
półokręgu 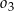 wybrano punkt
wybrano punkt 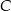 i na odcinkach
i na odcinkach 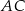 i
i 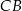 jako na średnicach skonstruowano półokręgi
jako na średnicach skonstruowano półokręgi 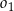 i
i 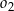 . Odcinek
. Odcinek 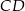 jest odcinkiem wspólnej stycznej półokręgów
jest odcinkiem wspólnej stycznej półokręgów 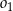 i
i 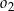 . Oblicz długość odcinka
. Oblicz długość odcinka 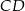 jeżeli promienie półokręgów
jeżeli promienie półokręgów 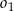 i
i 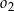 są odpowiednio równe
są odpowiednio równe 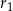 i
i 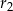 .
.
Wykaż, że dla dowolnej liczby 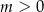 prawdziwa jest nierówność
prawdziwa jest nierówność 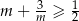 .
.
W nieskończonym ciągu arytmetycznym 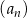 , określonym dla
, określonym dla 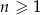 , suma dziewięciu początkowych wyrazów jest równa 171. Średnia arytmetyczna pierwszego, trzeciego i ósmego wyrazu tego ciągu, jest równa 15. Wyrazy
, suma dziewięciu początkowych wyrazów jest równa 171. Średnia arytmetyczna pierwszego, trzeciego i ósmego wyrazu tego ciągu, jest równa 15. Wyrazy 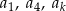 ciągu
ciągu 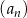 , w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny
, w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny 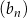 . Oblicz
. Oblicz 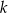 .
.

