/Szkoła średnia/Zadania maturalne
Planimetria – okręgi poziom rozszerzony
Dane są dwa okręgi o środkach w punktach 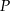 i
i 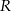 , styczne zewnętrznie w punkcie
, styczne zewnętrznie w punkcie 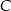 . Prosta
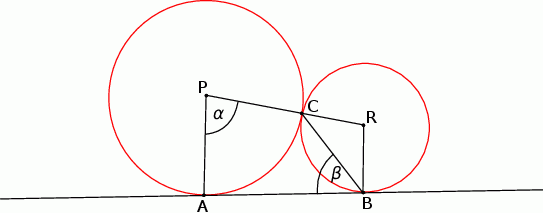
. Prosta 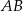 jest styczna do obu okręgów odpowiednio w punktach
jest styczna do obu okręgów odpowiednio w punktach 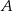 i
i 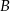 oraz
oraz 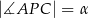 i
i 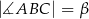 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 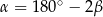 .
.
Odcinek 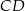 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 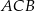 trójkąta
trójkąta 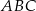 . Kąty trójkąta
. Kąty trójkąta 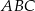 mają miary
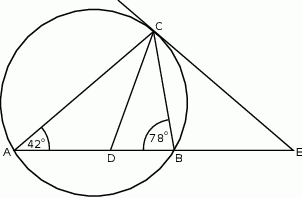
mają miary 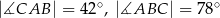 . Styczna do okręgu opisanego na tym trójkącie w punkcie
. Styczna do okręgu opisanego na tym trójkącie w punkcie 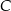 przecina prostą
przecina prostą 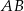 w punkcie
w punkcie 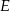 (zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta
(zobacz rysunek). Oblicz, ile stopni ma każdy z kątów trójkąta 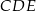 .
.
Na okręgu o środku 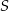 wybrano punkty
wybrano punkty 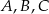 i
i 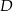 w ten sposób, że prosta
w ten sposób, że prosta 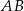 zawiera punkt
zawiera punkt 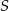 , a proste
, a proste 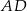 i
i 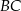 przecinają się w punkcie
przecinają się w punkcie 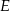 . Punkt
. Punkt 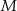 jest punktem wspólnym prostych
jest punktem wspólnym prostych 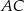 i
i 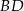 . Wykaż, że proste
. Wykaż, że proste 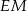 i
i  są prostopadłe.
są prostopadłe.
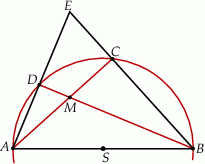
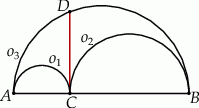
Na średnicy  półokręgu
półokręgu  wybrano punkt
wybrano punkt 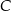 i na odcinkach
i na odcinkach 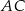 i
i 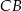 jako na średnicach skonstruowano półokręgi
jako na średnicach skonstruowano półokręgi 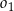 i
i 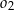 . Odcinek
. Odcinek 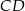 jest odcinkiem wspólnej stycznej półokręgów
jest odcinkiem wspólnej stycznej półokręgów 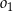 i
i 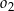 . Oblicz długość odcinka
. Oblicz długość odcinka 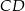 jeżeli promienie półokręgów
jeżeli promienie półokręgów 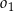 i
i 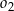 są odpowiednio równe
są odpowiednio równe 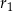 i
i 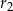 .
.
Do dwóch okręgów przecinających się w punktach 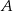 i
i 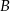 poprowadzono wspólną styczną
poprowadzono wspólną styczną 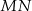 , przy czym punkt
, przy czym punkt 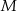 należy do pierwszego, a punkt
należy do pierwszego, a punkt 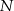 do drugiego okręgu. Wykaż, że prosta
do drugiego okręgu. Wykaż, że prosta 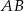 dzieli odcinek
dzieli odcinek 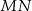 na połowy.
na połowy.
Przez środek 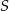 cięciwy
cięciwy 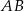 okręgu poprowadzono cięciwę
okręgu poprowadzono cięciwę 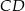 , przy czym
, przy czym 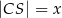 i
i 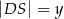 . Oblicz długość cięciwy
. Oblicz długość cięciwy 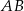 .
.
Odległości środków dwóch okręgów od wierzchołka kąta są równe 8 i 12. Okręgi te są styczne zewnętrznie i każdy z nich jest styczny do obu ramion kąta. Oblicz długości ich promieni.
Dwa okręgi przecinają się w punktach 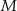 i
i 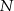 . Przez punkt
. Przez punkt 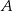 pierwszego okręgu prowadzimy proste
pierwszego okręgu prowadzimy proste 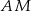 i
i 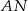 , przecinające drugi okrąg w punktach
, przecinające drugi okrąg w punktach 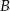 i
i 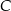 . Udowodnij, że styczna w punkcie
. Udowodnij, że styczna w punkcie 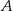 do pierwszego okręgu jest równoległa do prostej
do pierwszego okręgu jest równoległa do prostej 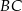 .
.
Okręgi o środkach odpowiednio 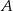 i
i 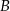 są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku
są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku 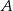 jest równy 1.
jest równy 1.
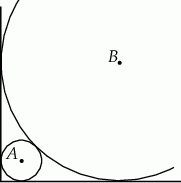
Uzasadnij, że promień okręgu o środku 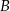 jest większy niż
jest większy niż 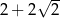 .
.
Dwa okręgi o promieniach  i
i 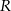 (
(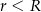 ) są styczne zewnętrznie. Prosta
) są styczne zewnętrznie. Prosta 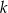 nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej
nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej 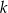 . Rozważ dwa przypadki.
. Rozważ dwa przypadki.

