/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Matura 2010
poziom podstawowy Informator CKE, zestaw 2 Czas pracy: 170 minut
Zadania zamknięte
Liczba 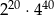 jest równa
jest równa
A) 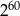 B)
B) 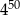 C)
C) 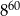 D)
D) 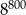
Zbiór rozwiązań nierówności 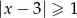 jest przedstawiony na rysunku
jest przedstawiony na rysunku
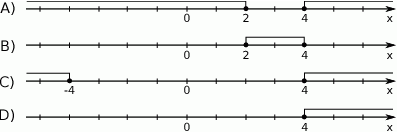
O zdarzeniach losowych 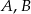 wiadomo, że:
wiadomo, że: 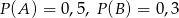 i
i 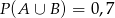 . Prawdopodobieństwo iloczynu zdarzeń
. Prawdopodobieństwo iloczynu zdarzeń 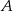 i
i 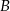 spełnia warunek
spełnia warunek
A) 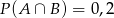 B)
B) 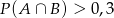 C)
C) 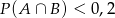 D)
D) 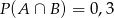
Wskaż liczbę, której 6% jest równe 6.
A) 0,36 B) 3,6 C) 10 D) 100
Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 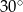 . Kąt rozwarty tego równoległoboku jest równy
. Kąt rozwarty tego równoległoboku jest równy
A) 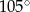 B)
B) 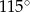 C)
C) 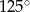 D)
D) 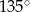
Funkcja 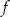 określona jest wzorem
określona jest wzorem
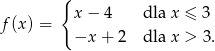
Ile miejsc zerowych ma ta funkcja?
A) 0 B) 1 C) 2 D) 3
Kąt  jest ostry i
jest ostry i 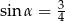 . Wówczas
. Wówczas
A) 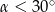 B)
B) 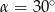 C)
C) 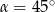 D)
D) 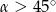
Liczba 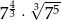 jest równa
jest równa
A) 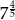 B)
B) 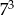 C)
C) 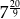 D)
D) 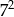
Dana jest funkcja 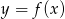 określona dla
określona dla 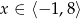 , której wykres jest przedstawiony na rysunku.
, której wykres jest przedstawiony na rysunku.
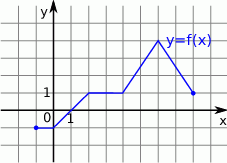
Wskaż zbiór wartości tej funkcji.
A) 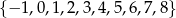 B)
B) 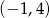 C)
C) 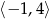 D)
D) 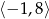
Trzeci wyraz ciągu geometrycznego jest równy 4, a piąty wyraz tego ciągu jest równy 1. Pierwszy wyraz tego ciągu jest równy
A) 4 B) 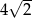 C)
C) 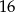 D)
D) 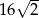
Pewien wielościan ma 6 krawędzi. Liczba jego ścian jest równa
A) 4 B) 5 C) 6 D) 9
Wykres funkcji kwadratowej 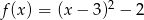 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 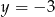 B)
B) 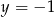 C)
C) 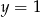 D)
D) 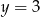
Odcinki 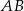 i
i 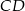 są równoległe. Długości odcinków
są równoległe. Długości odcinków 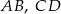 i
i 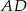 są podane na rysunku.
są podane na rysunku.
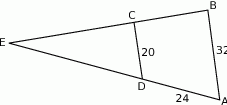
Długość odcinka 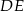 jest równa
jest równa
A) 44 B) 40 C) 36 D) 15
Wskaż równanie okręgu o środku 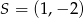 i promieniu
i promieniu 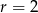 .
.
A) 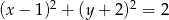
B) 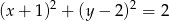
C) 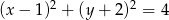
D) 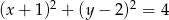
Równanie 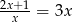
A) ma dwa rozwiązania: 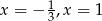
B) ma dwa rozwiązania: 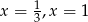
C) nie ma żadnego rozwiązania
D) ma tylko jedno rozwiązanie 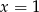
Suma długości wszystkich krawędzi sześcianu jest równa 24. Objętość tego sześcianu jest równa
A) 8 B) 27 C) 24 D) 64
Ciąg 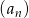 jest określony wzorem
jest określony wzorem 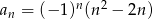 dla
dla 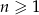 . Wtedy
. Wtedy
A) 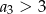 B)
B) 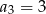 C)
C) 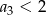 D)
D) 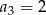
Liczba 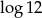 jest równa
jest równa
A) 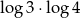 B)
B) 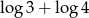 C)
C) 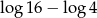 D)
D) 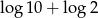
Zbiorem rozwiązań nierówności 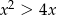 jest
jest
A) 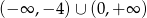 B)
B) 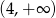 C)
C) 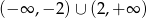 D)
D) 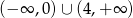
Prosta 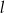 ma równanie
ma równanie 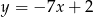 . Równanie prostej prostopadłej do
. Równanie prostej prostopadłej do 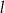 i przechodzącej przez punkt
i przechodzącej przez punkt 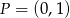 ma postać
ma postać
A) 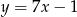 B)
B) 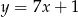 C)
C) 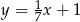 D)
D) 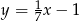
Zadania otwarte
Punkty 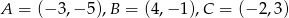 są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
Rozwiąż równanie 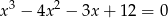 .
.
W trójkącie prostokątnym, w którym przyprostokątne mają długości 2 i 4, jeden z kątów ostrych ma miarę  . Oblicz
. Oblicz 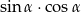 .
.
Uczeń otrzymał pięć ocen: 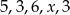 . Średnia arytmetyczna tych ocen jest równa 4. Oblicz
. Średnia arytmetyczna tych ocen jest równa 4. Oblicz  i medianę tych pięciu ocen.
i medianę tych pięciu ocen.
Liczby 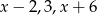 są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Oblicz  .
.
Do zbiornika o pojemności 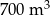 można doprowadzić wodę dwiema rurami. W ciągu jednej godziny pierwsza rura dostarcza do zbiornika o
można doprowadzić wodę dwiema rurami. W ciągu jednej godziny pierwsza rura dostarcza do zbiornika o 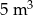 wody więcej niż druga rura. Czas napełniania zbiornika tylko pierwszą rurą jest o 16 godzin krótszy od czasu napełniania tego zbiornika tylko drugą rurą. Oblicz, w ciągu ilu godzin pusty zbiornik zostanie napełniony, jeśli woda będzie doprowadzana przez obie rury jednocześnie.
wody więcej niż druga rura. Czas napełniania zbiornika tylko pierwszą rurą jest o 16 godzin krótszy od czasu napełniania tego zbiornika tylko drugą rurą. Oblicz, w ciągu ilu godzin pusty zbiornik zostanie napełniony, jeśli woda będzie doprowadzana przez obie rury jednocześnie.
Rzucamy dwa razy symetryczną, sześcienną kostką, której jedna ściana ma jedno oczko, dwie ściany mają po dwa oczka i trzy ściany mają po trzy oczka. Oblicz prawdopodobieństwo zdarzenia: liczby oczek otrzymane w obu rzutach różnią się o 1.
Podstawą ostrosłupa 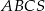 jest trójkąt równoboczny
jest trójkąt równoboczny 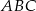 o boku długości 8. Punkt
o boku długości 8. Punkt 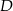 jest środkiem krawędzi
jest środkiem krawędzi 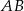 , odcinek
, odcinek 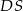 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 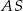 i
i 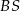 mają długość 7. Oblicz długość krawędzi
mają długość 7. Oblicz długość krawędzi 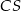 tego ostrosłupa.
tego ostrosłupa.
Punkt 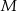 leży wewnątrz prostokąta
leży wewnątrz prostokąta 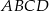 (zob. rysunek). Udowodnij, że
(zob. rysunek). Udowodnij, że 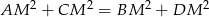 .
.