/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 28 marca 2015 Czas pracy: 170 minut
Zadania zamknięte
Przybliżenie dziesiętne liczby 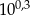 z dokładnością do czterech miejsc po przecinku jest równe 1,9953. Przybliżeniem dziesiętnym liczby
z dokładnością do czterech miejsc po przecinku jest równe 1,9953. Przybliżeniem dziesiętnym liczby 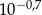 z dokładnością do 0,01 jest liczba
z dokładnością do 0,01 jest liczba
A) 0,02 B) 19,95 C) 0,19 D) 0,2
Dany jest okrąg o środku 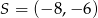 i promieniu 2015. Obrazem tego okręgu w symetrii osiowej względem osi
i promieniu 2015. Obrazem tego okręgu w symetrii osiowej względem osi 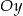 jest okrąg o środku w punkcie
jest okrąg o środku w punkcie 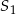 . Odległość między punktami
. Odległość między punktami 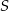 i
i 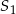 jest równa
jest równa
A) 12 B) 16 C) 2015 D) 4030
Rozwiązaniami równania 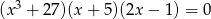 są liczby
są liczby
A) 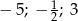 B)
B) 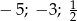 C)
C) 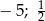 D)
D) 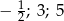
6% pewnej liczby jest równe 15. 14% tej liczby jest równe
A) 28 B) 36 C) 32 D) 35
Równość 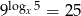 jest prawdziwa dla
jest prawdziwa dla
A) 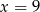 B)
B) 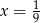 C)
C) 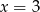 D)
D) 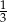
Wyrażenie 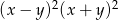 jest równe
jest równe
A) 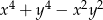 B)
B) 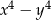 C)
C) 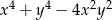 D)
D) 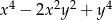
Funkcja 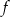 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący iloczynem dwóch różnych liczb pierwszych. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący iloczynem dwóch różnych liczb pierwszych. Spośród liczb: 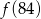 ,
, 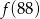 ,
, 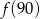 ,
, 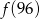 najmniejsza to
najmniejsza to
A) 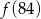 B)
B) 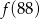 C)
C) 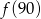 D)
D) 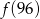
Zbiorem rozwiązań nierówności 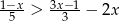 jest przedział
jest przedział
A) 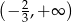 B)
B) 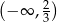 C)
C) 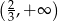 D)
D) 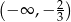
Na rysunku przedstawiony jest wykres funkcji 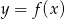 . Dziedziną funkcji
. Dziedziną funkcji 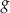 , gdzie
, gdzie 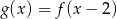 jest zbiór
jest zbiór
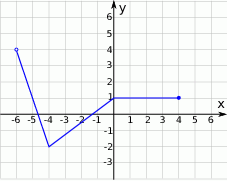
A) 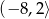 B)
B) 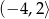 C)
C) 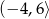 D)
D) 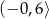
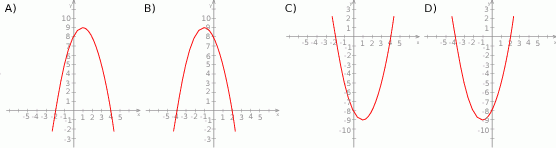
Wskaż rysunek, na którym przedstawiony jest wykres funkcji kwadratowej, określonej wzorem 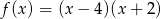 .
.
Liczba 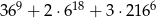 jest równa
jest równa
A) 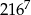 B)
B) 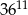 C)
C) 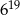 D)
D) 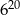
Wartość wyrażenia 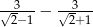 jest równa
jest równa
A) 0 B) 6 C) 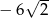 D)
D) 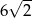
Samochód pokonał trasę długości 234 km w ciągu 39 minut. Gdyby samochód jadąc z tą samą prędkością średnią miał pokonać odległość 282 km, to zajęłoby to
A) 47 minut. B) 45 minut. C) 48 minut. D) 44 minuty.
Jeżeli kąt  jest ostry i
jest ostry i 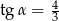 , to
, to 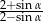 równa się
równa się
A) 1 B) 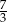 C) 3 D)
C) 3 D) 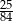
Wskaż 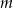 , dla którego funkcja liniowa
, dla którego funkcja liniowa 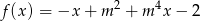 jest rosnąca.
jest rosnąca.
A) 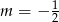 B)
B) 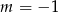 C)
C) 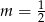 D)
D) 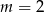
Dane jest równanie 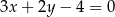 . Z którym z poniższych równań tworzy ono układ sprzeczny?
. Z którym z poniższych równań tworzy ono układ sprzeczny?
A) 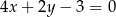 B)
B) 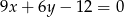 C)
C) 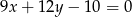 D)
D) 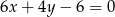
Wysokość trapezu równoramiennego o kącie ostrym 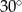 i ramieniu długości
i ramieniu długości 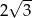 jest równa
jest równa
A) 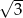 B) 3 C)
B) 3 C) 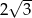 D) 2
D) 2
Pole powierzchni całkowitej czworościanu foremnego jest równe 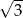 . Suma długości krawędzi tego czworościanu jest równa
. Suma długości krawędzi tego czworościanu jest równa
A) 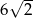 B) 3 C) 4 D) 6
B) 3 C) 4 D) 6
Odległość środka okręgu o średnicy 14 od prostej jest równa 7. Zatem liczba punktów wspólnych okręgu i prostej jest równa:
A) 0 B) 1 C) 2 D) 3
Średnia arytmetyczna zestawu danych: 4, 5, 3, 8, 10, 4, 8, 9, 6,  jest równa 6,5. Mediana tego zestawu jest równa
jest równa 6,5. Mediana tego zestawu jest równa
A) 5 B) 6 C) 7 D) 8
W ciągu geometrycznym 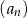 dane są:
dane są: 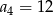 i
i 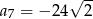 . Ciąg geometryczny
. Ciąg geometryczny 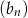 ma taki sam pierwszy wyraz jak ciąg
ma taki sam pierwszy wyraz jak ciąg 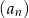 , ale jego iloraz jest dwukrotnością ilorazu ciągu
, ale jego iloraz jest dwukrotnością ilorazu ciągu 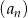 . Zatem
. Zatem
A) 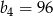 B)
B) 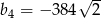 C)
C) 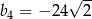 D)
D) 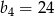
Ciąg 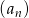 jest określony wzorem
jest określony wzorem 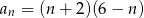 dla
dla 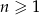 . Liczba dodatnich wyrazów tego ciągu jest równa
. Liczba dodatnich wyrazów tego ciągu jest równa
A) 3 B) 4 C) 6 D) 5
W klasie liczącej  osób, w tym 7 dziewcząt, wybrano losowo jedną osobę. Prawdopodobieństwo, że jest to chłopiec jest równe
osób, w tym 7 dziewcząt, wybrano losowo jedną osobę. Prawdopodobieństwo, że jest to chłopiec jest równe  , zatem:
, zatem:
A) 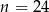 B)
B) 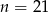 C)
C) 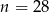 D)
D) 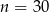
Na płaszczyźnie dany jest czworokąt 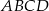 .
.
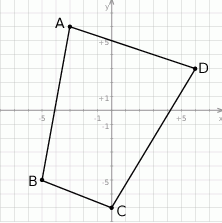
Który wierzchołek tego czworokąta jest położony najdalej od początku układu współrzędnych?
A) 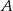 B)
B) 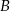 C)
C) 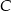 D)
D) 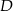
Ostrosłup i graniastosłup mają równe pola podstaw i równe wysokości. Objętość ostrosłupa jest równa 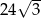 . Objętość graniastosłupa jest równa
. Objętość graniastosłupa jest równa
A) 8 B) 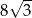 C)
C) 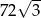 D) 72
D) 72
Zadania otwarte
Rozwiąż równanie 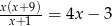 , dla
, dla 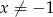 .
.
Ewa kupiła tablet za 480 zł oraz dodatkowe akcesoria w cenie 120 zł. Miesiąc później jej kolega Maciek kupił dokładnie taki sam tablet z akcesoriami, ale cena tabletu była o 10% niża, a cena akcesoriów wzrosła o 5%. O ile procent Maciek kupił swój zestaw taniej niż Ewa?
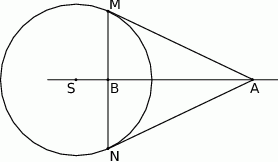
Na okręgu o promieniu  wybrano punkty
wybrano punkty 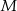 i
i 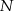 w ten sposób, że proste
w ten sposób, że proste 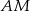 i
i 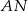 są styczne do okręgu. Punkt
są styczne do okręgu. Punkt 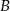 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 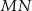 i prostej łączącej
i prostej łączącej 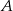 ze środkiem
ze środkiem 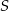 tego okręgu. Wykaż, że
tego okręgu. Wykaż, że 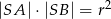 .
.
Szachownica do gry w szachy ma 64 pola. Przypuśćmy, że pierwsze pole ma wartość 1 grosza, drugie 2 groszy, trzecie 4 groszy, czwarte 8 groszy itd. Jaki jest jest najmniejszy numer pola szachownicy, którego wartość przekracza 1 000 000 zł?
Wyznacz liczbę naturalną  , dla której liczby
, dla której liczby 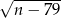 i
i 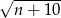 są kolejnymi liczbami naturalnymi.
są kolejnymi liczbami naturalnymi.
Na rysunku przedstawiono fragment wykresu funkcji 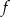 , który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem
, który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem 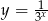 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  .
.
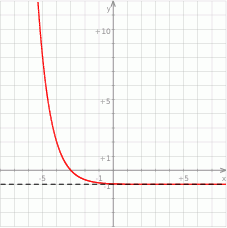
- Odczytaj z wykresu i zapisz zbiór tych wszystkich argumentów, dla których wartości funkcji
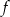 są jednocześnie większe od
są jednocześnie większe od 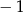 i mniejsze od 0.
i mniejsze od 0. - Podaj miejsce zerowe funkcji
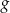 określonej wzorem
określonej wzorem 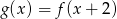 .
.
W zbiorniku zamontowano dwie pompy: pierwsza z nich służy do napełniania zbiornika, a druga do jego opróżniania. Pierwsza pompa napełnia cały zbiornik w ciągu 30 minut, a druga opróżnia cały zbiornik w ciągu 20 minut. W pustym zbiorniku uruchamiamy pierwszą pompę, a po 5 minutach jej pracy uruchamiamy również drugą pompę. Po ilu minutach zbiornik będzie ponownie pusty?
Punkt 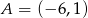 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 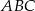 , a punkt
, a punkt 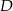 jest środkiem odcinka
jest środkiem odcinka 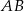 . Równania prostych
. Równania prostych 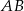 ,
, 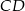 oraz symetralnej boku
oraz symetralnej boku 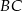 to odpowiednio
to odpowiednio 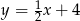 ,
, 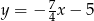 i
i 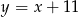 . Napisz równanie prostej zawierającej wysokość trójkąta
. Napisz równanie prostej zawierającej wysokość trójkąta 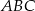 opuszczoną z wierzchołka
opuszczoną z wierzchołka 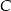 .
.
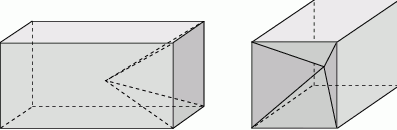
Z drewnianego prostopadłościanu o objętości 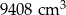 i podstawie będącej kwadratem o boku 14 cm, wycięto ostrosłup prawidłowy czworokątny o wysokości równej połowie najdłuższej krawędzi prostopadłościanu. Otrzymano w ten sposób bryłę, której widok z dwóch stron przedstawiono na rysunku. Oblicz pole powierzchni całkowitej otrzymanej bryły.
i podstawie będącej kwadratem o boku 14 cm, wycięto ostrosłup prawidłowy czworokątny o wysokości równej połowie najdłuższej krawędzi prostopadłościanu. Otrzymano w ten sposób bryłę, której widok z dwóch stron przedstawiono na rysunku. Oblicz pole powierzchni całkowitej otrzymanej bryły.