/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 17 marca 2012 Czas pracy: 170 minut
Zadania zamknięte
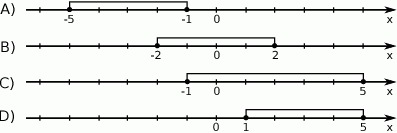
Który z zaznaczonych przedziałów jest zbiorem rozwiązań nierówności 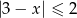 .
.
Cena książki wzrosła o 15% i wynosi 92 zł. Ile kosztowała książka przed podwyżką?
A) 105,8 zł B) 77 zł C) 78,2 zł D) 80 zł
Rozwiązaniem układu równań 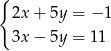 jest
jest
A) 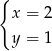 B)
B) 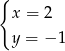 C)
C) 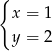 D)
D) 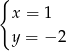
Dziedziną funkcji 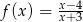 jest zbiór:
jest zbiór:
A) 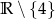 B)
B) 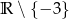 C)
C) 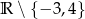 D)
D) 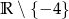
Liczba 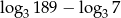 jest równa
jest równa
A) 1 B) 2 C) 3 D) 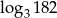
Dla pewnych liczb  i
i 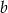 zachodzą równości:
zachodzą równości: 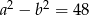 i
i 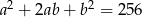 . Dla tych liczb
. Dla tych liczb  i
i 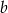 wartość wyrażenia
wartość wyrażenia 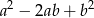 jest równa
jest równa
A) 9 B) 3 C) 18 D) 208
Najmniejszą liczbą całkowitą należącą do zbioru rozwiązań nierówności 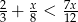 jest
jest
A) -1 B) -2 C) 1 D) 2
Wierzchołek paraboli o równaniu 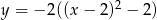 ma współrzędne
ma współrzędne
A) 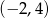 B)
B) 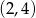 C)
C) 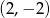 D)
D) 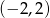
Na rysunku przedstawiony jest wykres funkcji liniowej 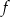 .
.
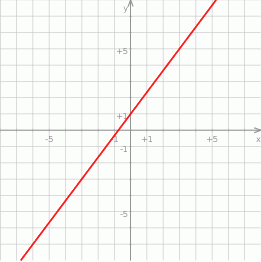
Funkcja 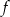 jest określona wzorem
jest określona wzorem
A) 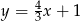 B)
B) 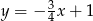 C)
C) 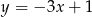 D)
D) 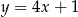
Dane są wielomiany 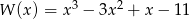 i
i 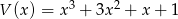 . Stopień wielomianu
. Stopień wielomianu 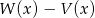 jest równy
jest równy
A) 0 B) 1 C) 2 D) 3
Funkcja liniowa określona jest wzorem 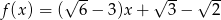 . Miejscem zerowym tej funkcji jest liczba
. Miejscem zerowym tej funkcji jest liczba
A) 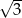 B)
B) 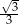 C)
C) 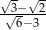 D)
D) 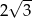
Dany jest nieskończony ciąg geometryczny 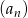 , w którym
, w którym 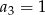 i
i 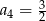 . Wtedy
. Wtedy
A) 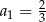 B)
B) 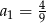 C)
C) 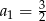 D)
D) 
Wyraz ogólny ciągu 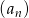 ma postać
ma postać 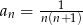 , gdzie
, gdzie 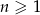 . Wobec tego
. Wobec tego
A) 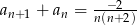
B) 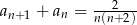
C) 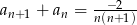
D) 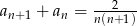
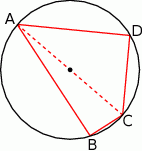
Czworokąt 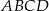 jest wpisany w okrąg, przy czym przekątna
jest wpisany w okrąg, przy czym przekątna 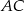 jest średnicą tego okręgu oraz
jest średnicą tego okręgu oraz 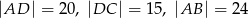 . Wtedy
. Wtedy
A) 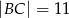 B)
B) 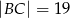 C)
C) 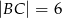 D)
D) 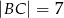
Kąt  jest ostry oraz
jest ostry oraz 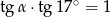 . Wtedy miara kąta
. Wtedy miara kąta  jest równa
jest równa
A) 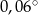 B)
B) 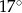 C)
C) 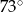 D)
D) 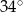
Pole trójkąta równobocznego o obwodzie 6 jest równe
A) 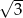 B)
B) 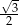 C)
C) 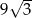 D)
D) 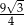
Średnia arytmetyczna siedmiu liczb: 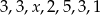 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 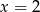 B)
B) 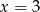 C)
C) 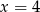 D)
D) 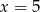
Styczną do okręgu 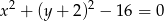 jest prosta o równaniu
jest prosta o równaniu
A) 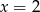 B)
B) 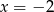 C)
C) 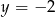 D)
D) 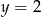
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 12 jest równa
A) 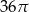 B)
B) 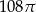 C)
C) 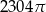 D)
D) 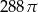
Punkty 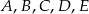 leżące na okręgu o środku
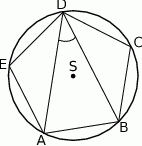
leżące na okręgu o środku 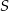 są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 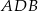 jest równa
jest równa
A) 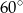 B)
B) 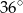 C)
C) 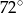 D)
D) 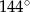
Ostrosłup ma 20 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 19 B) 40 C) 29 D) 38
Zadania otwarte
Rozwiąż równanie 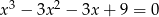 .
.
Wyznacz wszystkie liczby pierwsze spełniające nierówność 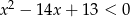 .
.
Liczby 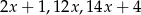 są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz  .
.
Kąt  jest ostry i
jest ostry i 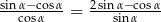 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 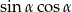 .
.
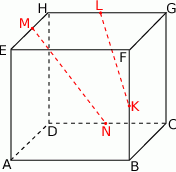
Punkty 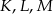 i
i 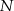 są środkami krawędzi
są środkami krawędzi 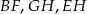 i
i 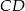 prostopadłościanu
prostopadłościanu 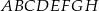 , w którym
, w którym 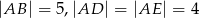 . Uzasadnij, że
. Uzasadnij, że 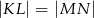 .
.
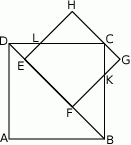
Bok 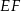 kwadratu
kwadratu 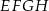 zawiera się w przekątnej
zawiera się w przekątnej 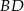 kwadratu
kwadratu 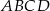 , a punkt
, a punkt 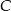 należy do odcinka
należy do odcinka 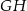 . Odcinki
. Odcinki 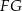 i
i 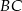 przecinają się w punkcie
przecinają się w punkcie 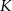 , a odcinki
, a odcinki 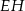 i
i 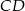 przecinają się w punkcie
przecinają się w punkcie 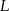 . Wykaż, że
. Wykaż, że 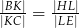 .
.
Napisz równanie okręgu przechodzącego przez punkt 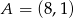 i stycznego do osi
i stycznego do osi 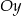 w punkcie
w punkcie 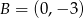 .
.
Ile jest liczb naturalnych czterocyfrowych, których zapis dziesiętny składa się tylko z dwóch różnych cyfr?
Pole każdej z dwóch prostokątnych działek jest równe 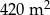 . Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 14 m mniejsza. Oblicz szerokość i długość każdej z działek.
. Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 14 m mniejsza. Oblicz szerokość i długość każdej z działek.
Podstawą ostrosłupa jest romb, którego przekątne mają długości 12 i 16. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych rombu w podstawie, a pole powierzchni bocznej jest równe 104. Oblicz objętość ostrosłupa.

