/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 9 kwietnia 2011 Czas pracy: 170 minut
Zadania zamknięte
Liczba 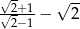 jest liczbą
jest liczbą
A) wymierną B) niewymierną C) mniejszą niż 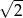 D) naturalną
D) naturalną
Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.
![]()
A) 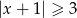 B)
B) 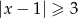 C)
C) 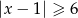 D)
D) 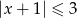
Liczba 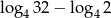 jest równa
jest równa
A) 4 B) 2 C) 3 D) 1
Narty kosztowały 680 zł. O ile procent należałoby obniżyć cenę nart, aby kosztowały 595 zł?
A) 8,5% B) 12,5% C) 14,2% D) 25%
Wyrażenie 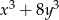 jest równe iloczynowi
jest równe iloczynowi
A) 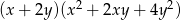
B) 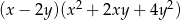
C) 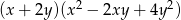
D) 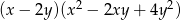
Wykres funkcji 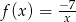 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i III B) II i IV C) I i III D) I i II
Funkcje 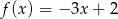 i
i 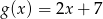 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 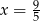 B)
B) 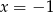 C)
C) 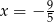 D)
D) 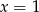
Wierzchołek paraboli o równaniu 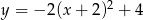 ma współrzędne
ma współrzędne
A) 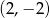 B)
B) 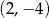 C)
C) 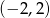 D)
D) 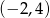
Zbiorem rozwiązań nierówności 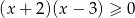 jest
jest
A) 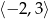
B) 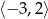
C) 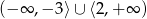
D) 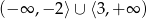
Wskaż 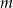 , dla którego funkcja liniowa
, dla którego funkcja liniowa 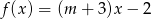 jest malejąca
jest malejąca
A) 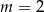 B)
B) 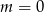 C)
C) 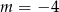 D)
D) 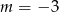
Który z podanych ciągów jest ciągiem geometrycznym?
A) 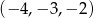 B)
B) 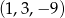 C)
C) 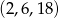 D)
D) 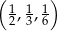
Dla 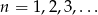 ciąg
ciąg 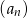 jest określony wzorem
jest określony wzorem 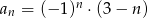 . Wtedy
. Wtedy
A) 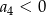 B)
B) 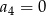 C)
C) 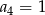 D)
D) 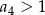
W ciągu arytmetycznym piąty wyraz jest równy 11, a dziewiąty jest równy 25. Różnica tego ciągu jest równa
A) 14 B) 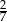 C) 7 D)
C) 7 D) 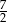
Kąt  jest ostry i
jest ostry i 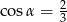 . Wartość wyrażenia
. Wartość wyrażenia 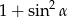 jest równa
jest równa
A) 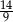 B)
B) 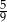 C)
C)  D)
D) 
Odcinki 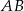 i
i 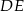 są równoległe. Długości odcinków
są równoległe. Długości odcinków 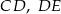 i
i 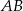 są odpowiednio równe 2, 4 i 16.
są odpowiednio równe 2, 4 i 16.
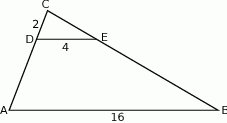
Długość odcinka 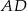 jest równa
jest równa
A) 12 B) 8 C) 3 D) 6
Środek 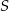 okręgu o równaniu
okręgu o równaniu 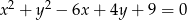 ma współrzędne
ma współrzędne
A) 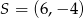 B)
B) 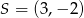 C)
C) 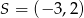 D)
D) 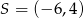
Wyniki konkursu ortograficznego podano w punktach: 82, 94, 88, 92, 90, 86, 76, 72. Medianą tego zestawu wyników jest
A) 86 B) 88 C) 87 D) 90
Objętość sześcianu jest równa 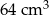 . Jaka jest suma długości wszystkich krawędzi tego sześcianu?
. Jaka jest suma długości wszystkich krawędzi tego sześcianu?
A) 48 cm B) 36 cm C) 24 cm D) 64 cm
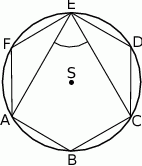
Punkty 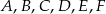 leżące na okręgu o środku
leżące na okręgu o środku 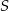 są wierzchołkami sześciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami sześciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 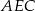 jest równa
jest równa
A) 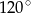 B)
B) 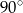 C)
C) 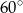 D)
D) 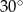
Prawdopodobieństwo zdarzenia 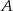 jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 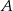 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 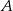 jest równe
jest równe
A) 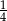 B)
B) 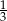 C)
C)  D)
D) 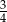
Zadania otwarte
Rozwiąż nierówność: 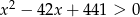 .
.
Przeciwprostokątna trójkąta prostokątnego jest dłuższa od jednej przyprostokątnej o 2 cm i od drugiej przyprostokątnej o 9 cm. Oblicz długości boków tego trójkąta.
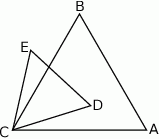
Trójkąty równoboczne 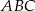 i
i 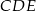 są położone tak, jak na poniższym rysunku. Wykaż, że
są położone tak, jak na poniższym rysunku. Wykaż, że 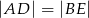 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 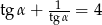 oblicz
oblicz 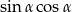 .
.
Wykaż, że jeżeli 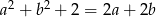 , to
, to 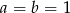 .
.
Ciąg 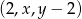 jest arytmetyczny, natomiast ciąg
jest arytmetyczny, natomiast ciąg 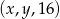 jest geometryczny. Oblicz
jest geometryczny. Oblicz  oraz
oraz 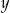 i podaj ten ciąg geometryczny.
i podaj ten ciąg geometryczny.
Punkty 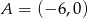 i
i 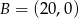 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 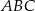 o przeciwprostokątnej
o przeciwprostokątnej 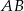 . Wierzchołek
. Wierzchołek 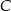 leży na prostej o równaniu
leży na prostej o równaniu 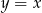 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 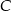 .
.
Oblicz objętość ostrosłupa prawidłowego trójkątnego o krawędzi podstawy długości 6 cm i krawędzi bocznej długości 8 cm.
Dwie prostokątne działki ogrodnicze mają odpowiednio pola powierzchni 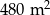 i
i 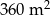 . Druga z działek jest o 2 metry węższa i o 4 metry krótsza od pierwszej działki. Oblicz, jakie wymiary mogą mieć działki. Podaj wszystkie możliwe odpowiedzi.
. Druga z działek jest o 2 metry węższa i o 4 metry krótsza od pierwszej działki. Oblicz, jakie wymiary mogą mieć działki. Podaj wszystkie możliwe odpowiedzi.

