/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 2 kwietnia 2022 Czas pracy: 180 minut
Zadania zamknięte
Wartość wyrażenia 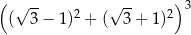 jest równa
jest równa
A) 512 B) 0 C) 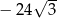 D)
D) 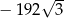
Granica 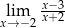
A) nie istnieje B) jest równa 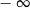 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 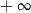
Wyrażenie 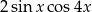 jest równe
jest równe
A) 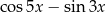 B)
B) 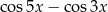 C)
C) 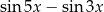 D)
D) 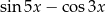
Liczba różnych pierwiastków równania 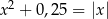 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Zadania otwarte
W wyniku dzielenia wielomianu 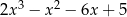 przez dwumian
przez dwumian 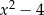 otrzymujemy resztę postaci
otrzymujemy resztę postaci 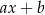 . Oblicz
. Oblicz  i
i 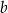 .
.
Dane są wektory ![→ a = [1,− 2]](https://img.zadania.info/zes/0050371/HzesT17x.gif) ,
, ![→ b = [− 2,− 1]](https://img.zadania.info/zes/0050371/HzesT18x.gif) ,
, ![→ c = [3,4]](https://img.zadania.info/zes/0050371/HzesT19x.gif) . Dobierz wartości parametrów
. Dobierz wartości parametrów 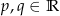 tak, aby wektory
tak, aby wektory 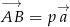 ,
, 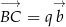 i
i 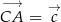 tworzyły trójkąt
tworzyły trójkąt 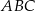 .
.
Wykaż, że jeżeli 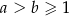 , to
, to 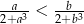 .
.
Dany jest trójkąt równoboczny 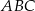 . Na bokach
. Na bokach 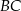 i
i 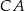 wybrano punkty – odpowiednio –
wybrano punkty – odpowiednio – 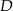 i
i 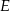 takie, że
takie, że 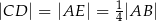 . Odcinki
. Odcinki 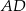 i
i 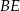 przecinają się w punkcie
przecinają się w punkcie 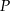 (zobacz rysunek).
(zobacz rysunek).
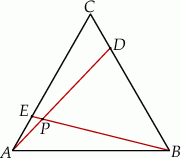
Wykaż, że pole trójkąta 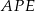 jest 52 razy mniejsze od pola trójkąta
jest 52 razy mniejsze od pola trójkąta 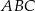 .
.
Dane są prosta 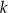 o równaniu
o równaniu 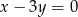 i prosta
i prosta 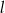 o równaniu
o równaniu 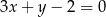 . Punkt
. Punkt 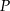 leży na prostej o równaniu
leży na prostej o równaniu 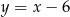 . Odległość punktu
. Odległość punktu 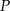 od prostej
od prostej 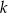 jest trzy razy większa niż odległość punktu
jest trzy razy większa niż odległość punktu 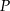 od prostej
od prostej 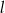 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 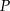 .
.
Suma czterech początkowych wyrazów ciągu 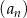 określonego dla
określonego dla 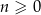 jest równa
jest równa 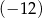 . Ponadto dla każdej liczby całkowitej
. Ponadto dla każdej liczby całkowitej 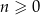 spełniony jest warunek
spełniony jest warunek 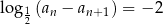 . Oblicz nieskończoną sumę
. Oblicz nieskończoną sumę
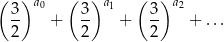
Odległość wierzchołka sześcianu od przekątnej sześcianu (do której dany wierzchołek nie należy) jest równa 4 cm. Oblicz objętość sześcianu.
Rozwiąż równanie 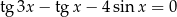 w przedziale
w przedziale 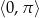 .
.
Trzy cięciwy okręgu o promieniu  tworzą trójkąt wpisany w ten okrąg. Dwie najkrótsze z tych cięciw mają długości
tworzą trójkąt wpisany w ten okrąg. Dwie najkrótsze z tych cięciw mają długości 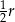 i
i 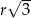 . Wykaż, że trzecia cięciwa ma długość
. Wykaż, że trzecia cięciwa ma długość 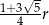 .
.
Dla jakich wartości parametru 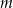 równanie
równanie 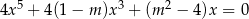 ma dokładnie trzy różne rozwiązania?
ma dokładnie trzy różne rozwiązania?
W każdej z czterech urn są 24 kule, w tym dokładnie 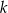 białych. Z każdej urny losujemy jedną kulę. Dla jakiej wartości
białych. Z każdej urny losujemy jedną kulę. Dla jakiej wartości 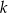 prawdopodobieństwo wylosowania dokładnie dwóch kul białych jest największe? Oblicz to największe prawdopodobieństwo.
prawdopodobieństwo wylosowania dokładnie dwóch kul białych jest największe? Oblicz to największe prawdopodobieństwo.

