/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 18 marca 2017 Czas pracy: 170 minut
Zadania zamknięte
Liczba 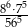 jest równa
jest równa
A) 8 B) 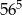 C) 7 D)
C) 7 D) 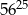
Liczba 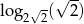 jest równa
jest równa
A) 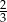 B)
B) 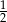 C)
C) 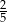 D)
D) 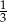
Na lokacie złożono 2000 zł przy rocznej stopie procentowej 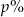 (procent składany). Odsetki naliczane są co pół roku. Po upływie dwóch lat wielkość kapitału na lokacie będzie równa
(procent składany). Odsetki naliczane są co pół roku. Po upływie dwóch lat wielkość kapitału na lokacie będzie równa
A) 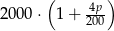 B)
B) 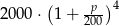 C)
C) 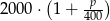 D)
D) 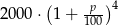
Liczba 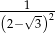 jest równa
jest równa
A) 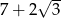 B)
B) 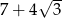 C)
C) 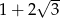 D)
D) 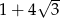
Najmniejszą liczbą całkowitą spełniającą nierówność 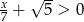 jest
jest
A) 15 B) 16 C) 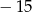 D)
D) 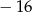
Proste o równaniach 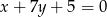 i
i 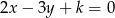 przecinają się na osi
przecinają się na osi 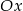 . Zatem parametr
. Zatem parametr 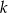 jest równy
jest równy
A) 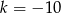 B)
B) 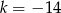 C)
C) 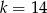 D)
D) 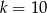
Spośród liczb, które są rozwiązaniami równania 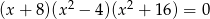 , wybrano największą i najmniejszą. Suma tych dwóch liczb jest równa
, wybrano największą i najmniejszą. Suma tych dwóch liczb jest równa
A) 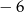 B)
B) 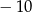 C) 6 D) 24
C) 6 D) 24
Pierwszy wyraz ciągu geometrycznego jest równy 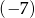 , a czwarty wyraz tego ciągu jest równy 875. Iloraz tego ciągu jest równy
, a czwarty wyraz tego ciągu jest równy 875. Iloraz tego ciągu jest równy
A) 294 B) 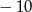 C)
C) 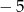 D)
D) 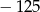
Sinus kąta ostrego równoległoboku jest równy  . Suma cosinusów wszystkich kątów wewnętrznych tego równoległoboku jest równa
. Suma cosinusów wszystkich kątów wewnętrznych tego równoległoboku jest równa
A) 0 B) 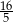 C)
C) 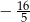 D)
D) 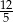
Informacja do zadań 10 i 11
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 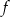 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 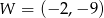 . Liczby
. Liczby 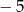 i 1 to miejsca zerowe funkcji
i 1 to miejsca zerowe funkcji 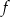 .
.
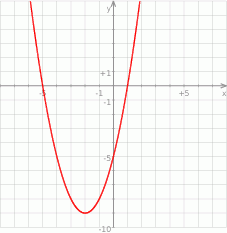
Zbiorem wartości funkcji 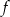 jest przedział
jest przedział
A) 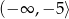 B)
B) 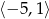 C)
C) 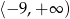 D)
D) 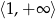
Największa wartość funkcji 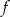 w przedziale
w przedziale 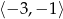 jest równa
jest równa
A) 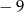 B)
B) 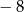 C)
C) 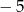 D) 0
D) 0
Wyrażenie 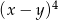 jest równe
jest równe
A) 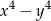
B) 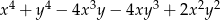
C) 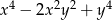
D) 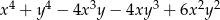
Jeżeli  jest liczbą ujemną i
jest liczbą ujemną i 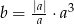 , to
, to
A) 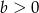 B)
B) 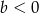 C)
C) 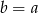 D)
D) 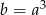
Na rysunku jest przedstawiona prosta zawierająca przekątną 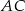 rombu
rombu 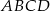 oraz wierzchołki
oraz wierzchołki 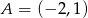 i
i 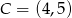 tego rombu.
tego rombu.
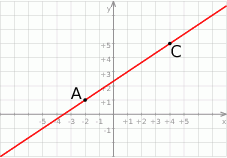
Wskaż równanie prostej zawierającej przekątną 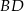 tego rombu.
tego rombu.
A) 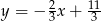 B)
B) 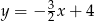 C)
C) 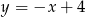 D)
D) 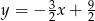
Ciąg 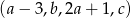 jest arytmetyczny i suma trzech jego początkowych wyrazów jest równa 78. Liczba
jest arytmetyczny i suma trzech jego początkowych wyrazów jest równa 78. Liczba  jest równa
jest równa
A) 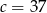 B)
B) 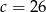 C)
C) 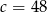 D)
D) 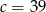
Wieża Eiffla ma wysokość 300 m, a pantofelek ma długość 0,3 mm. Ile razy wieża Eiffla jest wyższa od długości pantofelka?
A) 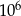 B)
B) 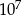 C) 1000 D)
C) 1000 D) 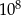
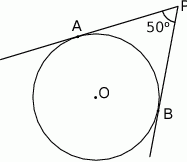
Punkty 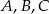 i
i 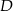 leżą na okręgu o środku
leżą na okręgu o środku 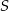 . Cięciwa
. Cięciwa 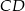 przecina średnicę
przecina średnicę 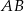 tego okręgu w punkcie
tego okręgu w punkcie 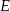 tak, że
tak, że 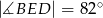 . Kąt środkowy
. Kąt środkowy 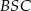 ma miarę
ma miarę 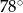 (zobacz rysunek).
(zobacz rysunek).
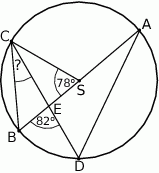
Kąt wpisany 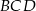 ma miarę
ma miarę
A) 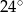 B)
B) 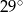 C)
C) 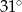 D)
D) 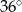
Z pudełka z metalowymi kulkami wyjęto najpierw 105 kulek, a potem 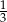 kulek, które pozostały w pudełku. W wyniku tych dwóch operacji liczba kulek w pudełku zmniejszyła się czterokrotnie. Ile kulek było początkowo w pudełku?
kulek, które pozostały w pudełku. W wyniku tych dwóch operacji liczba kulek w pudełku zmniejszyła się czterokrotnie. Ile kulek było początkowo w pudełku?
A) 171 B) 216 C) 168 D) 144
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 3 w punkcie 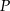 przechodzi przez środek okręgu o promieniu 4 (zobacz rysunek).
przechodzi przez środek okręgu o promieniu 4 (zobacz rysunek).
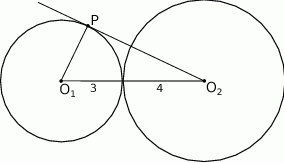
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności 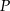 , jest równe
, jest równe
A) 21 B) 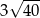 C)
C) 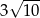 D) 24
D) 24
Do okręgu o środku 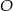 poprowadzono z zewnętrznego punktu
poprowadzono z zewnętrznego punktu 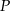 dwie styczne przecinające się w
dwie styczne przecinające się w 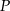 pod kątem
pod kątem 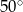 (zobacz rysunek). Punktami styczności są, odpowiednio, punkty
(zobacz rysunek). Punktami styczności są, odpowiednio, punkty 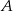 i
i 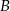 .
.
Kąt  ma miarę
ma miarę
A)  B)
B) 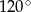 C)
C) 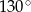 D)
D) 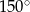
Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo zdarzenia polegającego na tym, że wynikiem rzutu jest co najmniej jedna reszka i trzy oczka na kostce, jest równe
A) 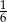 B)
B) 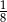 C)
C) 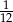 D)
D) 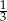
Średnia arytmetyczna czterech liczb: 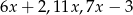 i
i 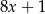 jest równa 88. Wynika stąd, że
jest równa 88. Wynika stąd, że
A) 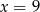 B)
B) 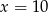 C)
C) 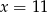 D)
D) 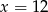
Średnica podstawy stożka ma długość 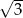 , a jego tworząca ma długość 1. Tangens kąta rozwarcia tego stożka jest równy
, a jego tworząca ma długość 1. Tangens kąta rozwarcia tego stożka jest równy
A) 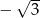 B)
B) 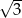 C)
C) 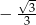 D)
D) 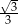
Ostrosłup ma tyle samo krawędzi bocznych, ile przekątnych ma jego podstawa. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 5 B) 6 C) 12 D) 10
Zadania otwarte
Rozwiąż nierówność 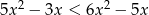 .
.
Wiedząc, że 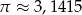 oblicz
oblicz 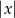 , gdzie
, gdzie 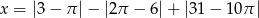 .
.
W skończonym ciągu arytmetycznym 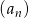 pierwszy wyraz
pierwszy wyraz 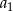 jest równy 9 oraz ostatni wyraz
jest równy 9 oraz ostatni wyraz 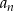 jest równy 93. Suma wszystkich wyrazów tego ciągu jest równa 2295. Oblicz, ile wyrazów ma ten ciąg.
jest równy 93. Suma wszystkich wyrazów tego ciągu jest równa 2295. Oblicz, ile wyrazów ma ten ciąg.
Udowodnij, że jeżeli liczby 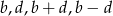 są różne od zera oraz
są różne od zera oraz 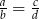 , to
, to 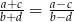 .
.
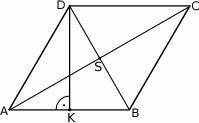
Przekątne rombu 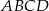 przecinają się w punkcie
przecinają się w punkcie 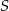 . Punkt
. Punkt 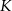 jest takim punktem boku
jest takim punktem boku 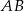 , że odcinek
, że odcinek 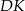 jest wysokością rombu (zobacz rysunek).
jest wysokością rombu (zobacz rysunek).
Wykaż, że jeżeli trójkąty 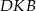 i
i 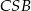 są przystające, to punkt
są przystające, to punkt 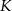 jest środkiem odcinka
jest środkiem odcinka 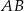 .
.
Mianownik ułamka jest dodatni i o 1 większy od licznika. Jeżeli do tego ułamka dodamy jego odwrotność to otrzymamy 2,05. Wyznacz ten ułamek.
W trapezie 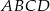 o podstawach
o podstawach 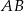 i
i 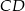 dane są długości przekątnych
dane są długości przekątnych 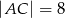 i
i 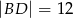 oraz pola
oraz pola 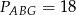 i
i 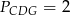 . Punkty
. Punkty 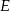 i
i 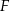 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 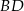 i
i 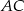 .
.
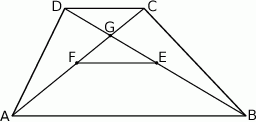
Oblicz pole trapezu  .
.
Niech 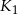 będzie sześcianem o krawędzi długości
będzie sześcianem o krawędzi długości  . Konstruujemy kolejno sześciany
. Konstruujemy kolejno sześciany 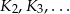 takie, że pole powierzchni całkowitej kolejnego sześcianu jest dwa razy większe od pola powierzchni poprzedniego sześcianu. Oblicz sumę objętości sześcianów
takie, że pole powierzchni całkowitej kolejnego sześcianu jest dwa razy większe od pola powierzchni poprzedniego sześcianu. Oblicz sumę objętości sześcianów 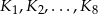 .
.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest o 85 większa od drugiej. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.

