/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki poziom podstawowy 3 listopada 2010 Czas pracy: 170 minut
Zadania zamknięte
Liczba 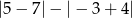 jest równa
jest równa
A) -3 B) -5 C) 1 D) 3
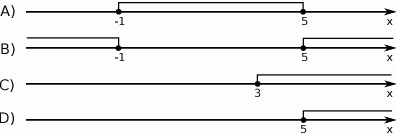
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 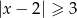 .
.
Samochód kosztował 30000 zł. Jego cenę obniżono o 10%, a następnie cenę po tej obniżce ponownie obniżono o 10%. Po tych obniżkach samochód kosztował
A) 24400 zł B) 24700 zł C) 24000 zł D) 24300 zł
Dana jest liczba 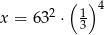 . Wtedy
. Wtedy
A) 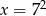 B)
B) 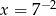 C)
C) 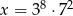 D)
D) 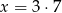
Kwadrat liczby 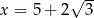 jest równy
jest równy
A) 37 B) 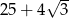 C)
C) 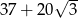 D) 147
D) 147
Liczba 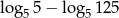 jest równa
jest równa
A) -2 B) -1 C) 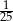 D) 4
D) 4
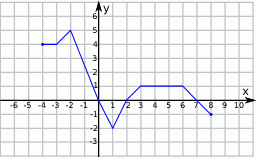
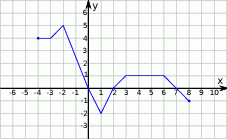
Zbiorem wartości funkcji 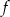 , której wykres przedstawiono poniżej jest
, której wykres przedstawiono poniżej jest
A) 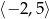 B)
B) 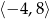 C)
C) 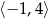 D)
D) 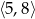
Korzystając z danego wykresu funkcji 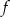 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą
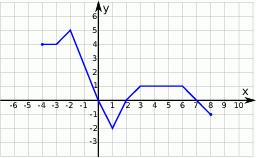
A) 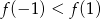 B)
B) 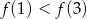 C)
C) 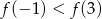 D)
D) 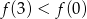
Rysunek przedstawia wykres funkcji  .
.
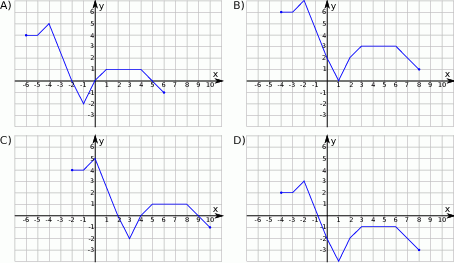
Wskaż wykres funkcji 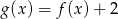 .
.
Liczby 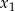 i
i 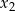 są pierwiastkami równania
są pierwiastkami równania 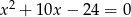 i
i 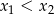 . Oblicz
. Oblicz 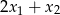 .
.
A) -22 B) -17 C) 8 D) 13
Liczba 2 jest pierwiastkiem wielomianu 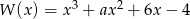 . Współczynnik
. Współczynnik  jest równy
jest równy
A) 2 B) -2 C) 4 D) -4
Wskaż 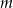 , dla którego funkcja liniowa określona wzorem
, dla którego funkcja liniowa określona wzorem 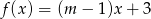 jest stała.
jest stała.
A) 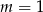 B)
B) 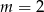 C)
C) 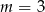 D)
D) 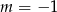
Zbiorem rozwiązań nierówności 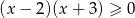 jest
jest
A) 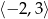
B) 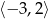
C) 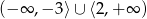
D) 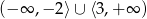
W ciągu geometrycznym 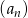 dane są:
dane są: 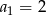 i
i 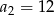 . Wtedy
. Wtedy
A) 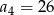 B)
B) 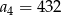 C)
C) 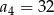 D)
D) 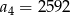
W ciągu arytmetycznym 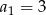 oraz
oraz 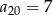 . Wtedy suma
. Wtedy suma 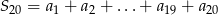 jest równa
jest równa
A) 95 B) 200 C) 230 D) 100
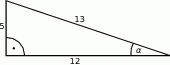
Na rysunku zaznaczono długości boków i kąt  trójkąta prostokątnego (zobacz rysunek). Wtedy
trójkąta prostokątnego (zobacz rysunek). Wtedy
A) 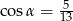 B)
B) 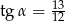 C)
C) 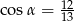 D)
D) 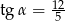
Ogród ma kształt prostokąta o bokach długości 20 m i 40 m. Na dwóch końcach przekątnej tego prostokąta wbito słupki. Odległość między tymi słupkami jest
A) równa 40 m
B) większa niż 50 m
C) większa niż 40 m i mniejsza niż 45 m
D) większa niż 45 m i mniejsza niż 50 m
Pionowy słupek o wysokości 90 cm rzuca cień o długości 60 cm. W tej samej chwili stojąca obok wieża rzuca cień długości 12 m. Jaka jest wysokość wieży?
A) 18 m B) 8 m C) 9 m D) 16 m
Punkty  i
i  leżą na okręgu o środku
leżą na okręgu o środku  (zobacz rysunek).
(zobacz rysunek).
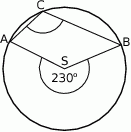
Miara zaznaczonego kąta wpisanego 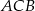 jest równa
jest równa
A) 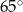 B)
B) 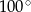 C)
C) 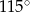 D)
D) 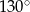
Dane są punkty 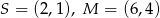 . Równanie okręgu o środku
. Równanie okręgu o środku 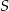 i przechodzącego przez punkt
i przechodzącego przez punkt 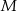 ma postać
ma postać
A) 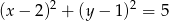
B) 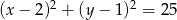
C) 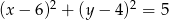
D) 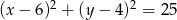
Proste o równaniach 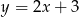 oraz
oraz 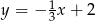
A) są równoległe i różne
B) są prostopadłe
C) przecinają się pod kątem innym niż prosty
D) pokrywają się
Wskaż równanie prostej, która jest osią symetrii paraboli o równaniu 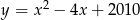 .
.
A) 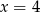 B)
B) 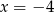 C)
C) 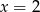 D)
D) 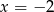
Kąt  jest ostry i
jest ostry i 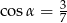 . Wtedy
. Wtedy
A) 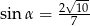 B)
B) 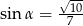 C)
C) 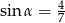 D)
D) 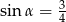
W karcie dań jest 5 zup i 4 drugie dania. Na ile sposobów można zamówić obiad składający się z jednej zupy i jednego drugiego dania?
A) 25 B) 20 C) 16 D) 9
W czterech rzutach sześcienną kostką do gry otrzymano następujące liczby oczek: 6, 3, 1, 4. Mediana tych danych jest równa
A) 2 B) 2,5 C) 5 D) 3,5
Zadania otwarte
Rozwiąż nierówność: 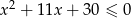 .
.
Rozwiąż równanie 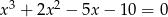 .
.
Przeciwprostokątna trójkąta prostokątnego jest dłuższa od jednej przyprostokątnej o 1 cm i od drugiej przyprostokątnej o 32 cm. Oblicz długości boków tego trójkąta.
Dany jest prostokąt 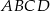 . Okręgi o średnicach
. Okręgi o średnicach 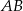 i
i 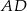 przecinają się w punktach
przecinają się w punktach 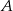 i
i 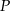 .
.
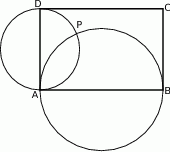
Wykaż, że punkty 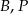 i
i  leżą na jednej prostej.
leżą na jednej prostej.
Uzasadnij, że jeśli 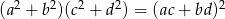 , to
, to 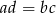 .
.
Oblicz, ile jest liczb naturalnych czterocyfrowych, w których zapisie pierwsza cyfra jest parzysta, a pozostałe nieparzyste.
Ciąg 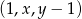 jest arytmetyczny, natomiast ciąg
jest arytmetyczny, natomiast ciąg 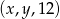 jest geometryczny. Oblicz
jest geometryczny. Oblicz  oraz
oraz  i podaj ten ciąg geometryczny.
i podaj ten ciąg geometryczny.
Punkty 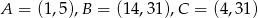 są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka 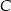 przecina prostą
przecina prostą 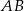 w punkcie
w punkcie 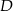 . Oblicz długość odcinka
. Oblicz długość odcinka 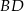 .
.
Droga z miasta 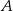 do miasta
do miasta 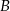 ma długość 474 km. Samochód jadący z miasta
ma długość 474 km. Samochód jadący z miasta 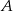 do miasta
do miasta 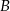 wyrusza godzinę później niż samochód z miasta
wyrusza godzinę później niż samochód z miasta 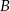 do miasta
do miasta 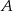 . Samochody te spotykają się w odległości 300 km od miasta
. Samochody te spotykają się w odległości 300 km od miasta 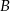 . Średnia prędkość samochodu, który wyjechał z miasta
. Średnia prędkość samochodu, który wyjechał z miasta 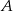 , liczona od chwili wyjazdu z
, liczona od chwili wyjazdu z 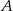 do momentu spotkania, była o 17 km/h mniejsza od średniej prędkości drugiego samochodu liczonej od chwili wyjazdu z
do momentu spotkania, była o 17 km/h mniejsza od średniej prędkości drugiego samochodu liczonej od chwili wyjazdu z 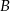 do chwili spotkania. Oblicz średnią prędkość każdego samochodu do chwili spotkania.
do chwili spotkania. Oblicz średnią prędkość każdego samochodu do chwili spotkania.

