/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki poziom rozszerzony
(stara formuła) 9 maja 2016 Czas pracy: 180 minut
Niech 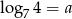 . Wyznacz
. Wyznacz 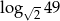 w zależności od
w zależności od  .
.
Wielomian 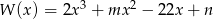 jest podzielny przez każdy z dwumianów
jest podzielny przez każdy z dwumianów 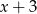 i
i 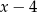 . Oblicz wartości współczynników
. Oblicz wartości współczynników  i
i 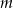 oraz rozwiąż nierówność
oraz rozwiąż nierówność 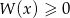 .
.
Rozwiąż równanie 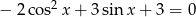 w przedziale
w przedziale 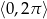 .
.
Ciąg 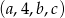 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 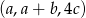 jest geometryczny. Oblicz
jest geometryczny. Oblicz 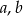 i
i  .
.
W trapezie równoramiennym 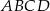 , w którym
, w którym 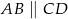 , dane są
, dane są 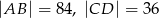 ,
, 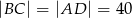 . Oblicz promień okręgu wpisanego w trójkąt
. Oblicz promień okręgu wpisanego w trójkąt 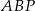 , gdzie
, gdzie 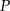 jest punktem przecięcia przekątnych tego trapezu.
jest punktem przecięcia przekątnych tego trapezu.
Punkty 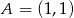 i
i 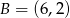 są wierzchołkami trójkąta
są wierzchołkami trójkąta 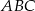 . Wysokości trójkąta
. Wysokości trójkąta 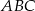 przecinają się w punkcie
przecinają się w punkcie 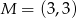 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
Reszta z dzielenia liczby naturalnej  przez 6 jest równa 1. Reszta z dzielenia liczby naturalnej
przez 6 jest równa 1. Reszta z dzielenia liczby naturalnej 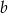 przez 6 jest równa 5. Uzasadnij, że liczba
przez 6 jest równa 5. Uzasadnij, że liczba 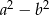 jest podzielna przez 24.
jest podzielna przez 24.
W ostrosłupie prawidłowym czworokątnym 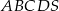 o podstawie
o podstawie 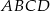 wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 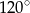 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
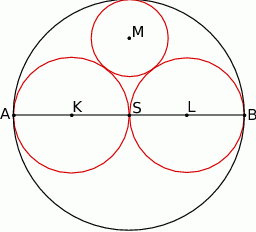
Dany jest okrąg o średnicy 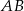 i środku
i środku 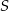 oraz dwa okręgi o średnicach
oraz dwa okręgi o średnicach 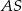 i
i 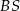 . Okrąg o środku
. Okrąg o środku 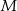 i promieniu
i promieniu  ma z każdym z danych okręgów dokładnie jeden punkt wspólny (zobacz rysunek). Wykaż, że
ma z każdym z danych okręgów dokładnie jeden punkt wspólny (zobacz rysunek). Wykaż, że 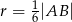 .
.
W urnie znajduje się 20 kul: 9 białych, 9 czerwonych i 2 zielone. Z tej urny losujemy bez zwracania 3 kule. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że co najmniej dwie z wylosowanych kul są tego samego koloru.
Rozpatrujemy wszystkie liczby naturalne dziesięciocyfrowe, w zapisie których mogą występować wyłącznie cyfry 1, 2, 3, przy czym cyfra 1 występuje dokładnie trzy razy. Uzasadnij, że takich liczb jest 15 360.

