/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom podstawowy 4 lutego 2013 Czas pracy: 170 minut
Zadania zamknięte
Wskaż liczbę, której 0,4% jest równe 12.
A) 0,048 B) 0,48 C) 30 D) 3000
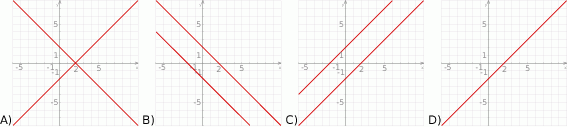
Dane są wielomiany 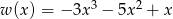 i
i 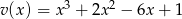 . Wówczas wielomian
. Wówczas wielomian 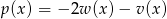 jest równy:
jest równy:
A) 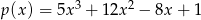
B) 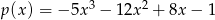
C) 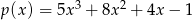
D) 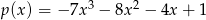
Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest przedział:
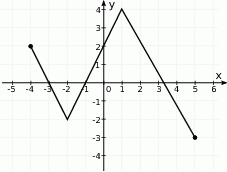
A) 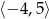 B)
B) 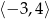 C)
C) 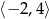 D)
D) 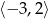
Który wyraz ciągu 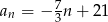 jest równy zero?
jest równy zero?
A) 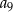 B)
B) 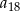 C)
C) 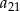 D)
D) 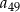
Przyprostokątne trójkąta prostokątnego mają długości 3 i 9. Sinus najmniejszego kąta tego trójkąta jest równy
A) 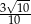 B)
B) 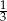 C)
C) 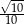 D)
D) 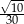
Wzorem funkcji kwadratowej 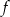 , której fragment wykresu przedstawiono na rysunku jest:
, której fragment wykresu przedstawiono na rysunku jest:
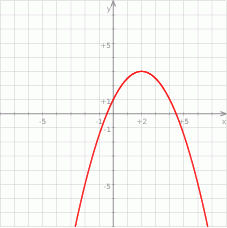
A) 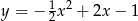 B)
B) 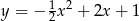 C)
C) 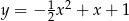 D)
D) 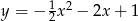
Wyrażenie 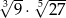 zapisane w postaci potęgi liczby 3 jest równe:
zapisane w postaci potęgi liczby 3 jest równe:
A) 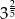 B)
B) 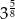 C)
C) 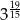 D)
D) 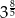
Interpretację geometryczną układu równań 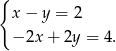 przedstawiono na rysunku:
przedstawiono na rysunku:
Wielomian 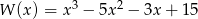 rozłożony na czynniki ma postać
rozłożony na czynniki ma postać
A) 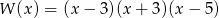
B) 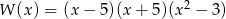
C) 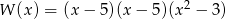
D) 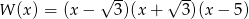
W loterii liczbowej wylosowano dziesięć liczb: 4, 3, 3, 3, 4, 6, 1, 5, 1, 6. Mediana tych danych jest równa
A) 5 B) 3,6 C) 3,5 D) 3
Punkt 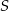 jest środkiem koła. Zatem miara kąta
jest środkiem koła. Zatem miara kąta  jest równa
jest równa
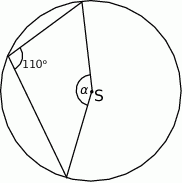
A) 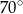 B)
B) 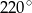 C)
C) 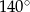 D)
D) 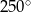
Prostymi równoległymi są wykresy funkcji liniowych:
A) 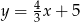 i
i 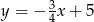
B) 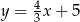 i
i 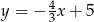
C) 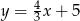 i
i 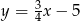
D) 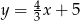 i
i 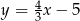
Liczba 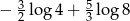 jest równa
jest równa
A) 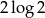 B)
B) 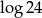 C) 2 D)
C) 2 D) 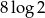
Dziedziną funkcji 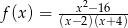 jest zbiór:
jest zbiór:
A) 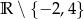 B)
B) 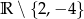 C)
C) 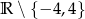 D)
D) 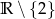
Zbiór rozwiązań nierówności 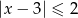 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
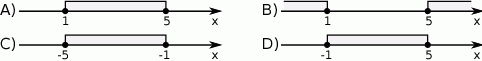
Rozwiązaniami równania 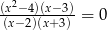 są liczby:
są liczby:
A) 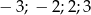 B)
B) 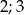 C)
C) 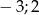 D)
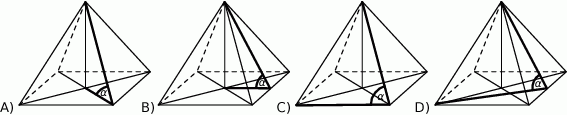
D) 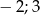
Kąt  nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
Do wykresu funkcji liniowej 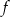 należą punkty
należą punkty 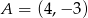 i
i 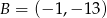 . Funkcja
. Funkcja 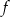 opisana jest wzorem
opisana jest wzorem
A) 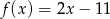 B)
B) 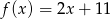 C)
C) 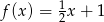 D)
D) 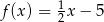
Ciągiem arytmetycznym jest ciąg o wyrazie ogólnym 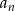 równym:
równym:
A) 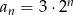 B)
B) 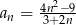 C)
C) 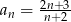 D)
D) 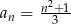
Wartość wyrażenia 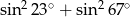 jest równa:
jest równa:
A) 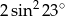 B)
B) 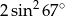 C) 1 D) 0
C) 1 D) 0
Wszystkich liczb trzycyfrowych parzystych, których cyfra jedności należy do zbioru 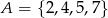 , cyfra dziesiątek do zbioru
, cyfra dziesiątek do zbioru 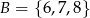 , a cyfra setek do zbioru
, a cyfra setek do zbioru 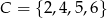 jest:
jest:
A) 48 B) 36 C) 24 D) 12
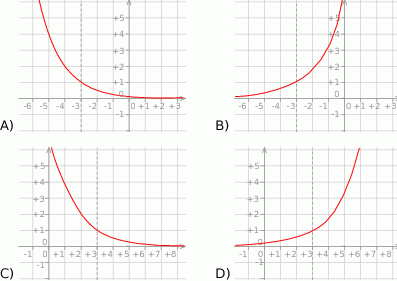
Wykres funkcji 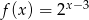 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
Dany jest okrąg o równaniu 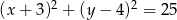 . Środkiem
. Środkiem 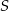 tego okręgu jest punkt:
tego okręgu jest punkt:
A) 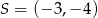 B)
B) 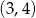 C)
C) 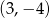 D)
D) 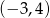
W trapezie miary kątów ostrych są równe 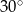 i
i  . Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
. Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
A) 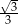 B)
B) 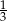 C)
C) 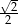 D)
D) 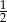
Największa wartość funkcji 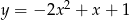 w przedziale
w przedziale 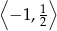 jest równa:
jest równa:
A) 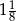 B) 1 C)
B) 1 C) 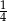 D)
D) 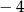
Zadania otwarte
Rozwiąż nierówność 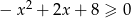 .
.
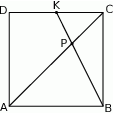
Na boku 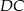 kwadratu
kwadratu 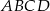 obrano punkt
obrano punkt 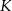 tak, że
tak, że 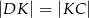 . Przekątna
. Przekątna 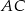 kwadratu przecina odcinek
kwadratu przecina odcinek 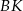 w punkcie
w punkcie 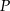 . Uzasadnij, że pole trójkąta
. Uzasadnij, że pole trójkąta 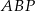 jest czterokrotnie większe niż pole trójkąta
jest czterokrotnie większe niż pole trójkąta 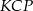 .
.
Oblicz pierwszy wyraz i iloraz ciągu geometrycznego wiedząc, że trzeci wyraz jest równy 18, a szósty 486.
Wykaż, że liczby 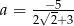 oraz
oraz 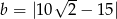 są liczbami przeciwnymi.
są liczbami przeciwnymi.
W trójkącie równoramiennym 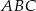 o podstawie
o podstawie 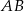 poprowadzono wysokość z wierzchołka
poprowadzono wysokość z wierzchołka 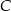 . Wyznacz równanie prostej zawierającej tę wysokość, jeśli
. Wyznacz równanie prostej zawierającej tę wysokość, jeśli 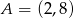 ,
, 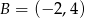 .
.
Ze zbioru liczb 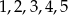 losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie bez zwracania tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 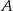 – otrzymana liczba jest mniejsza od 432.
– otrzymana liczba jest mniejsza od 432.
Z miast 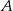 i
i 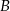 odległych o 330 km wyjechały naprzeciwko siebie dwa samochody. Samochód jadący z miasta
odległych o 330 km wyjechały naprzeciwko siebie dwa samochody. Samochód jadący z miasta 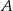 wyjechał 20 minut wcześniej i jechał z prędkością o 9 km/h mniejszą niż samochód jadący z miasta
wyjechał 20 minut wcześniej i jechał z prędkością o 9 km/h mniejszą niż samochód jadący z miasta 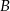 . Samochody te minęły się w odległości 168 km licząc od miasta
. Samochody te minęły się w odległości 168 km licząc od miasta 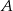 . Oblicz średnią prędkość każdego z samochodów.
. Oblicz średnią prędkość każdego z samochodów.
Oblicz pole i obwód rombu 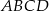 wiedząc, że przekątna
wiedząc, że przekątna 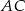 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 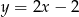 oraz
oraz 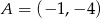 i
i 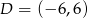 .
.
Metalowy stożek, którego tworząca o długości 10 jest nachylona do płaszczyzny podstawy pod kątem 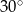 , przetopiono na sześć jednakowych kulek. Oblicz promień kulki.
, przetopiono na sześć jednakowych kulek. Oblicz promień kulki.

