/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom podstawowy 29 maja 2013 Czas pracy: 170 minut
Zadania zamknięte
Liczba 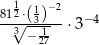 jest równa
jest równa
A) 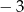 B)
B) 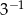 C)
C) 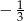 D) 3
D) 3
Wiadomo, że liczba 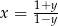 dla
dla 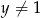 . Zatem
. Zatem
A) 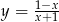 B)
B) 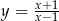 C)
C) 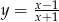 D)
D) 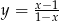
Liczbą odwrotną do 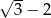 jest
jest
A) 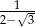 B)
B) 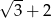 C)
C) 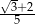 D)
D) 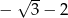
Jeżeli liczba  stanowi 40% dodatniej liczby
stanowi 40% dodatniej liczby 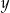 , to liczba
, to liczba 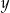 jest większa od liczby
jest większa od liczby  o:
o:
A) 60% B) 150% C) 160% D) 180%
Jaką liczbę należy podstawić zamiast litery  , aby równanie
, aby równanie 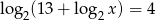 było prawdziwe?
było prawdziwe?
A) 8 B) 12 C) 16 D) 32
Wykresy funkcji liniowych 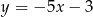 i
i 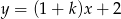 są prostymi prostopadłymi dla
są prostymi prostopadłymi dla
A) 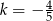 B)
B) 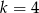 C)
C) 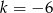 D)
D) 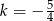
Rozwiązaniem nierówności 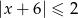 jest zbiór
jest zbiór
A) 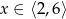 B)
B) 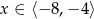 C)
C) 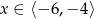 D)
D) 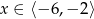
Wyrażenie 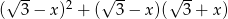 po uproszczeniu jest równe
po uproszczeniu jest równe
A) 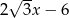 B)
B) 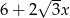 C)
C) 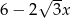 D)
D) 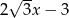
Iloraz ciągu geometrycznego 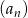 jest równy
jest równy 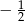 . Wynika stąd, że ciąg ten jest
. Wynika stąd, że ciąg ten jest
A) niemonotoniczny B) stały C) malejący D) rosnący
Wiadomo, że punkty 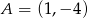 i
i 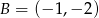 należą do prostej
należą do prostej 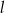 . Wówczas współczynnik kierunkowy prostej
. Wówczas współczynnik kierunkowy prostej 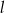 jest równy
jest równy
A) 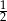 B) 1 C)
B) 1 C) 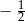 D)
D) 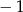
O ciągu arytmetycznym 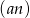 wiadomo, że
wiadomo, że 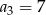 oraz
oraz 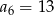 . Wynika stąd, że
. Wynika stąd, że
A) 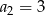 B)
B) 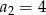 C)
C) 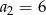 D)
D) 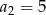
Jeżeli odcinki 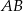 i
i 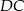 są równoległe, to długość odcinka
są równoległe, to długość odcinka 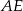 (patrz rys.) jest równa
(patrz rys.) jest równa
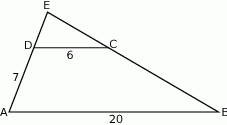
A) 9 B) 10 C) 11 D) 12
Jeżeli funkcja 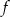 jest określona wzorem
jest określona wzorem 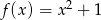 , to funkcję
, to funkcję 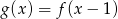 opisuje wzór
opisuje wzór
A) 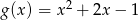
B) 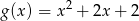
C) 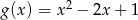
D) 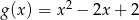
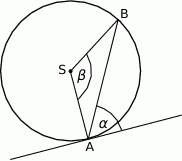
Kąt między cięciwą 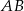 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 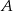 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 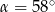 . Wówczas
. Wówczas
A) 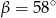 B)
B) 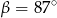 C)
C) 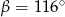 D)
D) 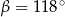
W trójkącie prostokątnym długość przeciwprostokątnej wynosi 8 i jednej z przyprostokątnych 6. Tangens mniejszego kąta ostrego tego trójkąta jest równy
A) 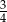 B)
B) 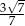 C)
C) 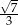 D)
D) 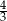
Kąt między ramionami trójkąta równoramiennego wynosi 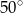 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 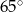 B)
B) 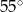 C)
C) 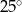 D)
D) 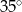
Suma dwudziestu początkowych wyrazów nieskończonego ciągu arytmetycznego 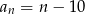 wynosi
wynosi
A) 8 B) 9 C) 10 D) 11
Pole trójkąta wyznaczonego przez wykresy funkcji 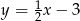 i
i 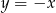 oraz oś
oraz oś 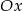 jest równe
jest równe
A) 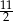 B)
B) 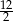 C)
C) 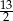 D)
D) 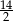
Jeżeli w ciągu geometrycznym 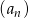 pierwszy wyraz ciągu jest równy
pierwszy wyraz ciągu jest równy 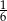 , a drugi wynosi
, a drugi wynosi 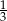 , to
, to
A) 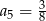 B)
B) 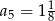 C)
C) 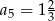 D)
D) 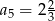
Wykres funkcji kwadratowej 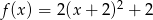 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 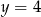 B)
B) 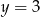 C)
C) 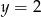 D)
D) 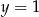
Funkcja
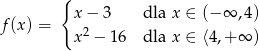
A) nie ma miejsc zerowych
B) ma dwa miejsce zerowe
C) ma jedno miejsca zerowe
D) ma trzy miejsca zerowe.
Punkty 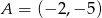 i
i 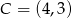 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 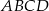 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 8 B) 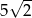 C) 5 D)
C) 5 D) 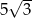
Dane są dwa wielomiany 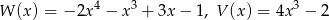 . Stopień wielomianu
. Stopień wielomianu 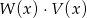 jest równy
jest równy
A) 12 B) 7 C) 4 D) 3
Zadania otwarte
Dla jakich argumentów funkcja 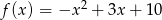 przyjmuje wartości nieujemne?
przyjmuje wartości nieujemne?
Przeciwprostokątna trójkąta prostokątnego jest dłuższa od jednej przyprostokątnej o 2 cm i od drugiej przyprostokątnej o 9 cm. Oblicz długości boków tego trójkąta.
Rozwiąż równanie 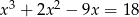 .
.
Asia wrzucała do skarbonki monety dwu i pięciozłotowe. Po przeliczeniu zawartości skarbonki okazało się, że w skarbonce znajdowało się 395 monet, a uzbierana kwota wynosi 1195 złotych. Oblicz ile monet każdego rodzaju było w skarbonce.
Udowodnij, że dla dowolnego kąta ostrego  prawdziwa jest nierówność
prawdziwa jest nierówność 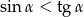 .
.
Oblicz pole rombu, w którym długość boku jest równa 13 cm, a długości przekątnych różnią się o 14 cm.
Dany jest trójkąt, w którym suma długości boku i wysokości opuszczonej na ten bok jest równa 8. Funkcja 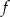 przyporządkowuje długości tego boku – pole trójkąta. Wyznacz wzór tej funkcji, jej dziedzinę, największą wartość, oraz zbiór wartości funkcji.
przyporządkowuje długości tego boku – pole trójkąta. Wyznacz wzór tej funkcji, jej dziedzinę, największą wartość, oraz zbiór wartości funkcji.
W trapezie równoramiennym przekątna ma długość 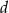 i tworzy z dłuższą podstawą kąt o mierze
i tworzy z dłuższą podstawą kąt o mierze  . Wykaż, że pole tego trapezu jest równe
. Wykaż, że pole tego trapezu jest równe 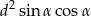 .
.
W dwóch szkołach wybudowano prostokątne baseny. W pierwszej z nich powierzchnia basenu wynosi 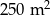 , w drugiej zaś jest o
, w drugiej zaś jest o 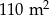 większa, a boki prostokąta odpowiednio dłuższe o 2 m na szerokości i o 5 m na długości basenu. Oblicz wymiary basenów w obu szkołach.
większa, a boki prostokąta odpowiednio dłuższe o 2 m na szerokości i o 5 m na długości basenu. Oblicz wymiary basenów w obu szkołach.

