/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom podstawowy grupa II 31 maja 2011 Czas pracy: 170 minut
Zadania zamknięte
Równanie 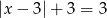 ma:
ma:
A) nieskończenie wiele rozwiązań
B) jedno rozwiązanie
C) dwa rozwiązania
D) zero rozwiązań
Wyrażenie 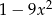 po rozłożeniu na czynniki liniowe ma postać:
po rozłożeniu na czynniki liniowe ma postać:
A) 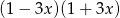 B)
B) 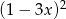 C)
C) 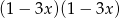 D)
D) 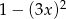
Dla której z liczb wyrażenie 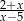 nie ma sensu liczbowego?
nie ma sensu liczbowego?
A) -2 B) 5 C) -5 D) 0
Wyznaczając 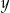 z równania
z równania 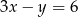 otrzymujemy:
otrzymujemy:
A) 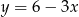 B)
B) 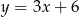 C)
C) 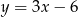 D)
D) 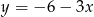
Która z poniższych liczb jest równa ułamkowi: 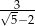 ?
?
A) 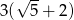 B)
B) 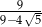 C)
C) 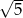 D) 9
D) 9
Do naczynia o pojemności 2,5 l i wlano 0,75 l wody. Jaki procent tego naczynia stanowi objętość wody?
A) 3% B) 60% C) 30% D) 3,(3)%
Obwód prostokąta jest równy 32 cm, a jeden z jego boków jest 3 razy dłuższy od drugiego boku. Pole tego prostokąta jest równe:
A) 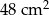 B)
B) 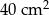 C)
C) 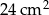 D)
D) 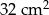
Jeżeli 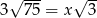 to liczba
to liczba  jest równa
jest równa
A) 15 B) 25 C) 5 D) 75
Liczba 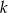 jest średnią arytmetyczną liczb
jest średnią arytmetyczną liczb 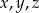 . Wynika stąd, że
. Wynika stąd, że
A) 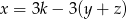 B)
B) 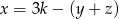 C)
C) 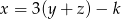 D)
D) 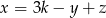
Odcinek podzielono na dwie części w stosunku 1:3. Ile procent całego odcinka stanowi większa jego część?
A) 25% B) 75% C) 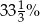 D)
D) 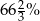
Suma kwadratów liczb 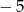 i
i 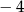 jest równa:
jest równa:
A) 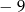 B) 81 C)
B) 81 C) 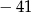 D) 41
D) 41
Długościami boków trójkąta mogą być odcinki:
A) 5 cm, 8 cm, 2 cm B) 7 cm, 9 cm, 10 cm C) 9 cm, 4 cm, 4 cm D) 3 cm, 2 cm, 1 cm
W kwadrat wpisano okrąg o promieniu 6 cm. Obwód tego kwadratu jest równy:
A) 48 cm B) 12 cm C) 24 cm D) 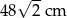
Miara kąta wewnętrznego ośmiokąta foremnego jest równa:
A)  B)
B) 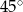 C)
C) 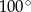 D)
D) 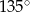
Rozwiązaniem równania 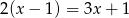 jest liczba:
jest liczba:
A) -2 B) -3 C) 1 D) 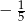
Wyrażenie 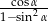 można zapisać w postaci:
można zapisać w postaci:
A) 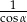 B)
B) 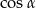 C)
C) 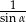 D)
D) 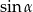
Długość boku trójkąta równobocznego o wysokości 6 cm jest równa:
A) 12 cm B) 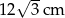 C)
C) 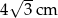 D)
D) 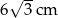
Wartość wyrażenia 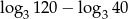 jest równa:
jest równa:
A) 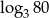 B) 0 C)
B) 0 C) 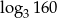 D) 1
D) 1
Dla 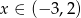 wyrażenie
wyrażenie 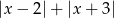 jest równe:
jest równe:
A) 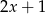 B) 5 C) -5 D) 1
B) 5 C) -5 D) 1
Wyrażenie 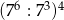 jest równe
jest równe
A) 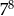 B)
B) 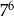 C)
C) 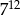 D)
D) 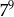
Prosta prostopadła do prostej 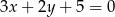 ma równanie:
ma równanie:
A) 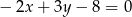 B)
B) 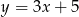 C)
C) 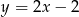 D)
D) 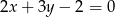
Prosta równoległa do prostej 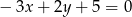 ma równanie:
ma równanie:
A) 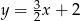 B)
B) 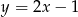 C)
C) 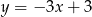 D)
D) 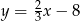
Punkt 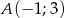 należy do wykresu funkcji:
należy do wykresu funkcji:
A) 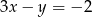 B)
B) 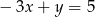 C)
C) 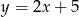 D)
D) 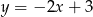
Jaką miarę ma kąt  ?
?
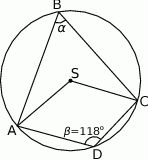
A) 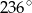 B)
B) 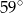 C)
C) 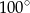 D)
D) 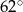
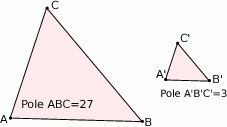
Znajdź skalę podobieństwa trójkąta 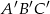 do trójkąta
do trójkąta 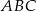 :
:
A) 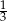 B)
B) 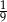 C) 3 D) 9
C) 3 D) 9
Zadania otwarte
Znajdź ułamek o mianowniku 5 leżący na osi liczbowej między 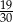 a
a 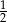 .
.
Znajdź wszystkie liczby całkowite, które nie spełniają nierówności 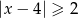 .
.
W trójkącie równobocznym 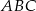 o boku długości
o boku długości  i wysokości
i wysokości 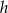 obrano punkt
obrano punkt 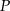 , z którego poprowadzono odcinki prostopadłe do boków tego trójkąta. Wykaż, że suma długości tych odcinków jest równa długości
, z którego poprowadzono odcinki prostopadłe do boków tego trójkąta. Wykaż, że suma długości tych odcinków jest równa długości 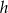 .
.
Wykaż, że liczba 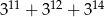 jest podzielna przez 31.
jest podzielna przez 31.
Oblicz pole rombu, którego jeden z kątów wewnętrznych wynosi 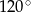 , a przekątna poprowadzona z wierzchołka tego kąta ma długość 10 cm.
, a przekątna poprowadzona z wierzchołka tego kąta ma długość 10 cm.
Na mapie o skali 1:50 000 las ma powierzchnię 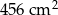 . Jaką rzeczywistą powierzchnię ma las?
. Jaką rzeczywistą powierzchnię ma las?
W klasie na początku roku było 30 uczniów. W ciągu roku z klasy odeszło 20% dziewcząt i przybyło 60% chłopców. Na koniec roku liczba dziewcząt i chłopców w klasie była równa. Ile dziewcząt, i ilu chłopców liczyła klasa na początku roku?
Dana jest funkcja 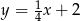 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt
. Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 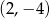 . Wykonaj rysunek do zadania.
. Wykonaj rysunek do zadania.
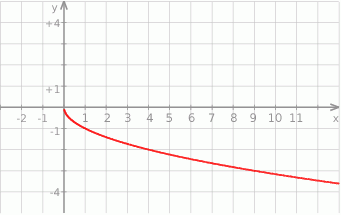
Korzystając z wykresu 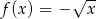 , naszkicuj wykres funkcji
, naszkicuj wykres funkcji 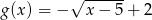 , a następnie odczytaj z wykresu: dziedzinę, zbiór wartości, oraz przedziały w których funkcja
, a następnie odczytaj z wykresu: dziedzinę, zbiór wartości, oraz przedziały w których funkcja 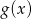 przyjmuje wartości dodatnie.
przyjmuje wartości dodatnie.