/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 28 lutego 2015 Czas pracy: 170 minut
Zadania zamknięte
Przybliżenie z niedomiarem liczby dodatniej  wynosi 18. Błąd względny tego przybliżenia wynosi 0,04. Wobec tego
wynosi 18. Błąd względny tego przybliżenia wynosi 0,04. Wobec tego
A) 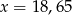 B)
B) 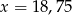 C)
C) 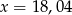 D)
D) 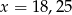
Okrąg o środku 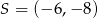 i promieniu 32 przekształcono najpierw w symetrii względem osi
i promieniu 32 przekształcono najpierw w symetrii względem osi 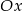 , a potem w symetrii względem osi
, a potem w symetrii względem osi 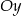 . W wyniku tych przekształceń otrzymano okrąg o środku
. W wyniku tych przekształceń otrzymano okrąg o środku 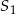 . Odległość między punktami
. Odległość między punktami 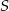 i
i 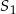 jest równa
jest równa
A) 20 B) 16 C) 10 D) 64
Dane są liczby 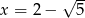 i
i 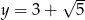 . Iloraz
. Iloraz 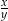 można zapisać w postaci:
można zapisać w postaci:
A) 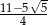 B)
B) 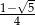 C)
C) 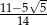 D)
D) 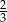
Liczba rozwiązań równania 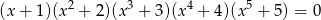 jest równa
jest równa
A) 9 B) 5 C) 3 D) 1
Funkcja wykładnicza określona wzorem 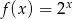 przyjmuje wartość 3 dla argumentu
przyjmuje wartość 3 dla argumentu
A) 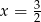 B)
B) 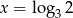 C)
C) 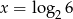 D)
D) 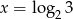
Wyrażenie 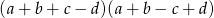 może być zapisane w postaci
może być zapisane w postaci
A) 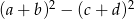
B) 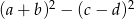
C) 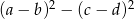
D) 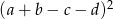
Połową odwrotności sześcianu liczby 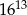 jest
jest
A) 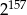 B)
B) 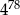 C)
C) 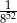 D)
D) 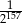
Równania 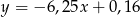 oraz
oraz 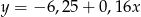 opisują dwie proste
opisują dwie proste
A) przecinające się pod kątem o mierze 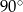 .
.
B) pokrywające się.
C) przecinające się pod kątem różnym od 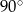 .
.
D) równoległe i różne.
W klasie IIF jest dziewięć dziewczynek, które stanowią 37,5% wszystkich uczniów tej klasy. Ilu chłopców jest w tej klasie?
A) 12 B) 15 C) 24 D) 16
Na rysunku przedstawiony jest wykres funkcji 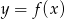 .
.

Najmniejszą wartością funkcji 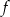 jest
jest
A) 3 B) 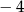 C)
C) 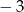 D) 7
D) 7
Funkcja 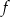 przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od
przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od  . Liczba
. Liczba 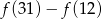 jest równa
jest równa
A) 5 B) 6 C) 4 D) 10
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 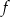 .
.
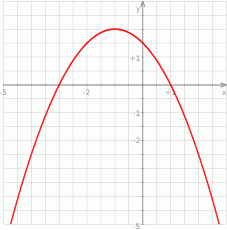
Funkcja 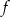 jest określona wzorem
jest określona wzorem
A) 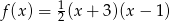
B) 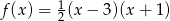
C) 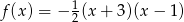
D) 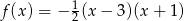
Siedmiocyfrowe numery telefonów w pewnym mieście są tworzone z cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, przy czym numery nie mogą zaczynać się od cyfr 0, 1, 9. Ile najwięcej takich numerów telefonicznych można utworzyć?
A) 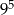 B)
B) 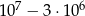 C)
C) 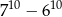 D)
D) 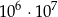
Kąt  jest ostry oraz
jest ostry oraz 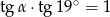 . Wtedy miara kąta
. Wtedy miara kąta  jest równa
jest równa
A) 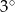 B)
B) 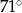 C)
C) 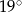 D)
D) 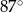
Punkty 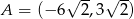 i
i 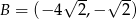 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 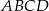 , którego przekątne przecinają się w punkcie
, którego przekątne przecinają się w punkcie 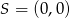 . Środek boku
. Środek boku 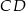 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 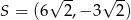 B)
B) 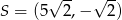 C)
C) 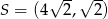 D)
D) 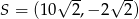
Wskaż układ, który ma nieskończenie wiele rozwiązań.
A) 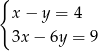 B)
B) 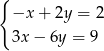 C)
C) 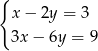 D)
D) 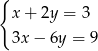
Wykonując rozmowę telefoniczną płacimy 43 grosze za rozpoczęcie połączenia oraz 32 grosze za każdą minutę połączenia. Ile minut trwała rozmowa, której łączny koszt wyniósł 12,59 zł?
A) 39 B) 37 C) 38 D) 44
Walec i stożek mają równe promienie podstaw, a wysokość walca jest dwa razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 3 B) 6 C) 2 D) 12
Na okręgu o środku 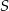 leżą punkty
leżą punkty 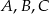 i
i 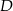 . Odcinek
. Odcinek 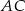 jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą
jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą 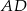 jest równy
jest równy 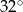 (zobacz rysunek).
(zobacz rysunek).
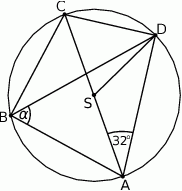
Kąt  między cięciwami
między cięciwami 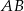 i
i 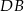 jest równy
jest równy
A) 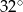 B)
B) 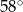 C)
C) 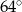 D)
D) 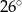
Odcinki 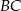 i
i 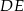 są równoległe i
są równoległe i 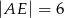 ,
, 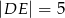 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 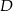 jest środkiem odcinka
jest środkiem odcinka 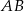 . Długość odcinka
. Długość odcinka 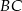 jest równa
jest równa
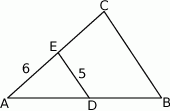
A) 10 B) 6 C) 8 D) 30
Jaką liczbę można wstawić pomiędzy liczby 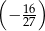 i
i 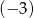 , aby z danymi liczbami tworzyła ciąg geometryczny?
, aby z danymi liczbami tworzyła ciąg geometryczny?
A) 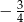 B)
B) 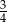 C)
C) 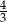 D)
D) 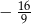
Ciąg 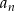 dany jest wzorem
dany jest wzorem 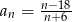 , gdzie
, gdzie 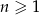 . Liczba wyrazów całkowitych tego ciągu to
. Liczba wyrazów całkowitych tego ciągu to
A) 2 B) 3 C) 4 D) 6
Losujemy jedną liczbę ze zbioru 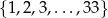 . Niech
. Niech 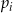 oznacza prawdopodobieństwo otrzymania liczby dającej resztę
oznacza prawdopodobieństwo otrzymania liczby dającej resztę 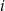 przy dzieleniu przez 10. Wtedy
przy dzieleniu przez 10. Wtedy
A) 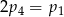 B)
B) 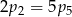 C)
C) 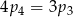 D)
D) 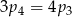
Jeżeli dodamy do siebie liczby wierzchołków, krawędzi i ścian ostrosłupa to otrzymamy 54. Ile krawędzi ma ten ostrosłup?
A) 26 B) 13 C) 28 D) 14
Dla której z przedstawionych serii danych mediana jest równa 4?
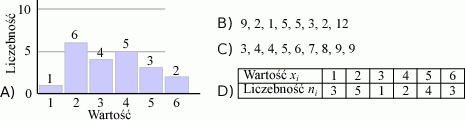
Zadania otwarte
Rozwiąż nierówność 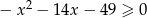 .
.
Rozwiąż równanie 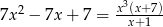 , dla
, dla 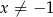 .
.
Uzasadnij, że liczba 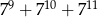 jest podzielna przez 399.
jest podzielna przez 399.
Wartość prędkości średniej obliczamy jako iloraz drogi i czasu, w którym ta droga została przebyta. Samochód przejechał z miejscowości 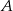 do miejscowości
do miejscowości 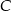 przez miejscowość
przez miejscowość 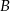 , która znajduje się w
, która znajduje się w 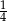 drogi z
drogi z 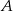 do
do 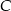 . Wartość prędkości średniej samochodu na trasie z
. Wartość prędkości średniej samochodu na trasie z 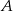 do
do 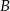 była równa 80 km/h, a na trasie z
była równa 80 km/h, a na trasie z 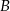 do
do 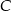 – 60 km/h. Oblicz wartość prędkości średniej samochodu na całej trasie z
– 60 km/h. Oblicz wartość prędkości średniej samochodu na całej trasie z 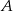 do
do 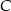 .
.
Wykaż, że jeżeli pole trójkąta prostokątnego jest równe 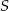 , to długość jego przeciwprostokątnej jest nie mniejsza niż
, to długość jego przeciwprostokątnej jest nie mniejsza niż 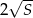 .
.
Oblicz miarę kąta ostrego, którego ramiona są zawarte w prostych o równaniach 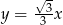 i
i 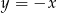 .
.
Kasia miała w skarbonce same monety jednozłotowe i dwuzłotowe, łącznie 186 zł. Gdy Kasia kupiła nową piłkę za 38 zł, to okazało się, że monet jednozłotowych pozostało jej dwa razy mniej, niż na początku miała monet dwuzłotowych, a monet dwuzłotowych pozostało jej tyle, ile na początku miała monet jednozłotowych. Jakimi monetami Kasia zapłaciła za piłkę?
Dany jest ostrosłup prawidłowy czworokątny 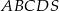 o podstawie
o podstawie 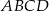 . Krawędź boczna tego ostrosłupa jest o
. Krawędź boczna tego ostrosłupa jest o 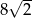 dłuższa od krawędzi podstawy, a wysokość ostrosłupa jest równa 14. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
dłuższa od krawędzi podstawy, a wysokość ostrosłupa jest równa 14. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
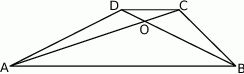
W trapezie 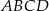 (
(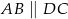 ) przekątne
) przekątne 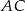 i
i 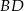 przecinają się w punkcie
przecinają się w punkcie 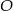 takim, że
takim, że 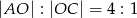 . Pole trójkąta
. Pole trójkąta 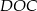 jest równe 2. Uzasadnij, że pole trapezu
jest równe 2. Uzasadnij, że pole trapezu 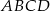 jest równe 50.
jest równe 50.