/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 30 kwietnia 2011 Czas pracy: 170 minut
Zadania zamknięte
Cena towaru bez podatku VAT jest równa 90 zł. Towar ten wraz z podatkiem VAT w wysokości 23% kosztuje
A) 91,23 zł B) 110,7 zł C) 69,3 zł D) 105,13 zł
Liczba 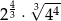 jest równa
jest równa
A) 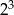 B)
B) 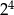 C)
C) 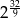 D)
D) 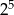
Liczba 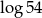 jest równa
jest równa
A) 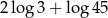 B)
B) 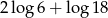 C)
C) 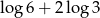 D)
D) 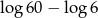
Kwadrat liczby 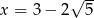 jest równy
jest równy
A) 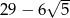 B)
B) 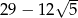 C)
C) 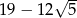 D) 29
D) 29
Dane są wielomiany 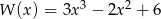 oraz
oraz 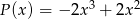 . Wielomian
. Wielomian 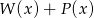 jest równy
jest równy
A) 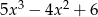
B) 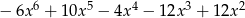
C) 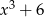
D) 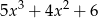
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 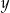 jest dodatnia. Wartość ujemną przyjmuje wyrażenie
jest dodatnia. Wartość ujemną przyjmuje wyrażenie
A) 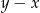 B)
B) 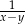 C)
C) 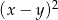 D)
D) 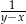
Do zbioru rozwiązań nierówności 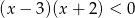 należy liczba
należy liczba
A) -3 B) 2 C) 3 D) -2
Jeżeli 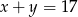 i
i 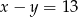 to
to
A) 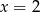 B)
B) 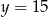 C)
C) 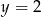 D)
D) 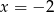
Wykres funkcji liniowej określonej wzorem 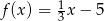 jest prostą prostopadłą do prostej o równaniu:
jest prostą prostopadłą do prostej o równaniu:
A) 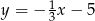 B)
B) 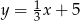 C)
C) 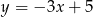 D)
D) 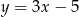
Kąt  jest kątem ostrym i
jest kątem ostrym i 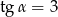 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 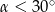 B)
B) 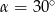 C)
C) 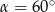 D)
D) 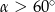
Wykres funkcji 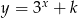 przechodzi przez punkt
przechodzi przez punkt 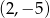 gdy liczba
gdy liczba 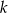 jest równa
jest równa
A) 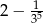 B) 4 C) -14 D) 14
B) 4 C) -14 D) 14
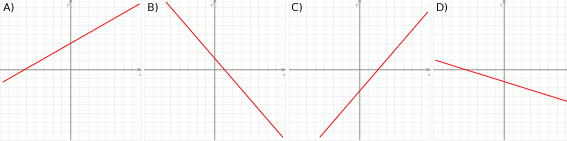
Na którym rysunku przedstawiono wykres funkcji liniowej 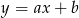 takiej, że
takiej, że 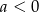 i
i 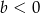 ?
?
W ciągu arytmetycznym o różnicy 5 ósmy wyraz wynosi 37. Pierwszy wyraz tego ciągu jest równy
A) 7 B) 13 C) 2 D) -3
W ciągu geometrycznym 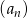 dane są:
dane są: 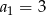 i
i 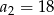 . Wtedy
. Wtedy
A) 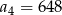 B)
B) 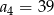 C)
C) 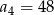 D)
D) 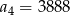
Okrąg opisany na kwadracie ma promień 8. Długość boku tego kwadratu jest równa
A) 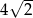 B)
B) 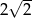 C)
C) 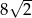 D) 8
D) 8
Podstawą ostrosłupa czworokątnego jest kwadrat o boku 5. Krawędź boczna o długości 6 jest prostopadła do podstawy. Objętość tego ostrosłupa wynosi:
A) 30 B) 150 C) 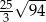 D) 50
D) 50
Na rysunku zaznaczono długości boków i kąt  trójkąta prostokątnego (zobacz rysunek). Wtedy
trójkąta prostokątnego (zobacz rysunek). Wtedy
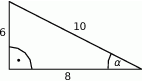
A) 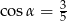 B)
B) 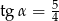 C)
C) 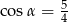 D)
D) 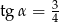
Wskaż równanie prostej, która jest osią symetrii paraboli o równaniu 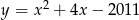 .
.
A) 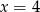 B)
B) 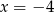 C)
C) 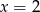 D)
D) 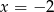
W trapezie równoramiennym kąt ostry ma miarę 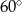 , a podstawy mają długości 12 i 6. Wysokość tego trapezu jest równa
, a podstawy mają długości 12 i 6. Wysokość tego trapezu jest równa
A) 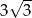 B)
B) 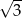 C)
C) 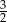 D)
D) 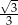
Dane są punkty 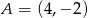 oraz
oraz 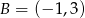 . Długość odcinka
. Długość odcinka 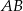 jest równa
jest równa
A) 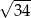 B)
B) 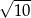 C)
C) 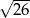 D)
D) 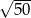
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 4.
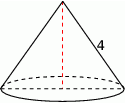
Pole powierzchni bocznej tego stożka jest równe
A) 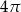 B)
B) 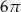 C)
C) 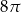 D)
D) 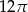
Ze zbioru liczb 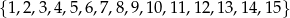 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 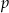 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 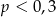 B)
B) 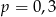 C)
C) 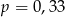 D)
D) 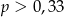
Zadania otwarte
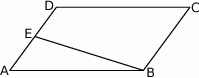
Punkt 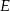 jest środkiem boku
jest środkiem boku 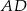 równoległoboku
równoległoboku 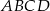 . Pole trójkąta
. Pole trójkąta 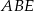 jest równe 2. Oblicz pole równoległoboku.
jest równe 2. Oblicz pole równoległoboku.
Wyznacz największą wartość funkcji 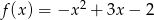 w przedziale
w przedziale 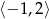 .
.
Rozwiąż równanie 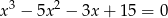 .
.
Wyznacz równania stycznych do okręgu 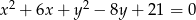 równoległych do osi
równoległych do osi 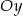 .
.
W jednej urnie są 4 kule: czerwona, biała, niebieska i zielona, a w drugiej urnie są 3 kule: czerwona, biała i zielona. Losujemy po jednej kuli z każdej urny. Jakie jest prawdopodobieństwo wyciągnięcia dwóch kul w tym samym kolorze?
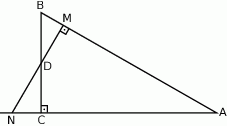
Przez środek 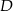 przyprostokątnej
przyprostokątnej 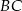 trójkąta prostokątnego
trójkąta prostokątnego 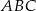 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 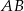 . Prosta ta przecina proste
. Prosta ta przecina proste 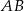 i
i 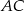 odpowiednio w punktach
odpowiednio w punktach 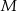 i
i 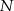 . Wykaż, że
. Wykaż, że 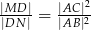 .
.
Punkty 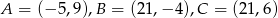 są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka  przecina prostą
przecina prostą 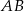 w punkcie
w punkcie 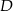 . Oblicz długość odcinka
. Oblicz długość odcinka 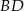 .
.
Pole trójkąta prostokątnego jest równe 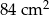 . Jedna przyprostokątna jest o 17 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
. Jedna przyprostokątna jest o 17 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
Podstawą ostrosłupa 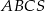 jest trójkąt równoboczny
jest trójkąt równoboczny 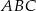 o boku długości 6. Punkt
o boku długości 6. Punkt 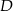 jest środkiem krawędzi
jest środkiem krawędzi 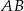 , odcinek
, odcinek 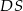 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 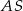 i
i 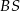 mają długość
mają długość 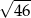 . Oblicz długość krawędzi
. Oblicz długość krawędzi 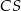 tego ostrosłupa.
tego ostrosłupa.

