/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 28 kwietnia 2012 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

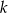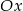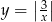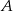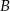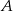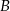Prosta k równoległa do osi Ox przecina wykres funkcji ||-3|| y = x w dwóch punktach A i B . Wyznacz współrzędne punktów A i B jeżeli wiadomo, że razem z punktem 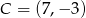C = (7,− 3) tworzą trójkąt o polu 12.

Zadanie 2
(4 pkt)

Wykaż, że liczba 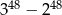48 48 3 − 2 jest podzielna przez 13.

Zadanie 3
(4 pkt)

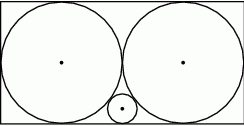
W prostokąt wpisano trzy parami styczne okręgi w ten sposób, że dwa z nich są styczne do trzech boków, prostokąta, a trzeci jest styczny do jednego z boków prostokąta (patrz rysunek). Oblicz promień mniejszego okręgu jeżeli promień większego okręgu jest równy 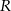R .

PIC

Zadanie 4
(4 pkt)

Wyznacz zbiór wartości funkcji 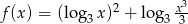3 f(x) = (log 3x)2 + log3 x3- zdefiniowanej na przedziale (1 ,+∞ ) .

Zadanie 5
(6 pkt)

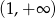Wielomian 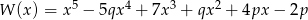W (x) = x5 − 5qx4 + 7x 3 + qx 2 + 4px − 2p jest podzielny przez wielomian 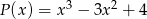P (x) = x3 − 3x 2 + 4 . Wyznacz 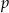p i q .

Zadanie 6
(5 pkt)

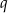Rozwiąż równanie 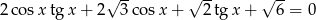√ -- √ -- √ -- 2 cos xtg x+ 2 3co sx + 2 tg x + 6 = 0 w zbiorze ⟨0,2π ⟩ .

Zadanie 7
(4 pkt)

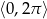Podstawy trapezu mają długości 9 i 12. Oblicz długość odcinka łączącego środki przekątnych tego trapezu.

Zadanie 8
(4 pkt)

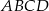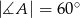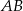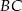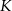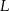Kąt ostry rombu ABCD ma miarę |∡A | = 60∘ . Na bokach AB i BC wybrano punkty K i L w ten sposób, że 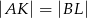|AK | = |BL | . Uzasadnij, że trójkąt 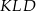KLD jest trójkątem równobocznym.

Zadanie 9
(4 pkt)

Ile jest liczb sześciocyfrowych liczb naturalnych, które mają cztery cyfry parzyste i dwie nieparzyste?

Zadanie 10
(5 pkt)

Na paraboli o równaniu 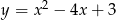2 y = x − 4x+ 3 wyznacz punkt, którego odległość od prostej 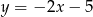y = − 2x − 5 jest najmniejsza.

Zadanie 11
(6 pkt)

W stożek o promieniu podstawy długości 6 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz promień podstawy walca, jeżeli jego objętość stanowi 4 9 objętości stożka.

Arkusz Wersja PDF
Rozwiązania