/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony
(technikum) 18 kwietnia 2015 Czas pracy: 180 minut
Na rysunku przedstawiony jest fragment wykresu funkcji określonej wzorem 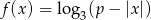 .
.
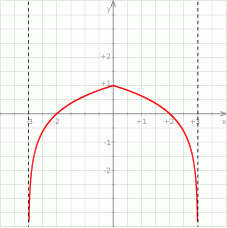
- Podaj wartość
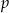 .
. - Naszkicuj wykres funkcji
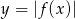 .
. - Podaj w zależności od parametru
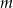 liczbę rozwiązań równania
liczbę rozwiązań równania 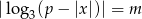 .
.
W trójkącie prostokątnym 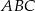 przyprostokątne mają długości
przyprostokątne mają długości 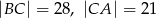 . Na boku
. Na boku 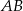 wybrano punkt
wybrano punkt 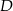 tak, że pole trójkąta
tak, że pole trójkąta 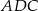 jest równe 126. Oblicz długość promienia okręgu opisanego na trójkącie
jest równe 126. Oblicz długość promienia okręgu opisanego na trójkącie 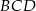 .
.
Wyznacz wszystkie wartości parametru 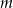 , dla których równanie
, dla których równanie 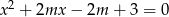 ma dwa różne pierwiastki należące do przedziału
ma dwa różne pierwiastki należące do przedziału 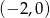 .
.
Kąty 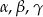 trójkąta
trójkąta 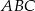 spełniają zależność
spełniają zależność
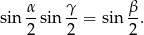
Oblicz wartość wyrażenia 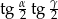 .
.
Wyznacz resztę z dzielenia wielomianu 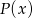 przez trójmian
przez trójmian 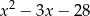 jeśli
jeśli 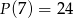 i
i 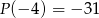 .
.
Do dwóch okręgów przecinających się w punktach 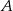 i
i 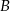 poprowadzono wspólną styczną
poprowadzono wspólną styczną 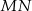 , przy czym punkt
, przy czym punkt 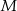 należy do pierwszego, a punkt
należy do pierwszego, a punkt 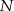 do drugiego okręgu. Wykaż, że prosta
do drugiego okręgu. Wykaż, że prosta 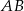 dzieli odcinek
dzieli odcinek 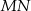 na połowy.
na połowy.
Liczby 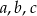 mają tę własność, że każdy z ciągów:
mają tę własność, że każdy z ciągów: 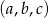 ,
, 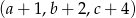 i
i 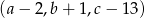 jest ciągiem geometrycznym. Oblicz
jest ciągiem geometrycznym. Oblicz 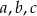 .
.
W pewnym budynku biurowym przydzielono pracownikom pięciocyfrowe kody bezpieczeństwa, przy czym każdy kod musiał spełniać następujące dwa warunki:
(1) kod musi zawierać co najmniej 3 różne cyfry
(2) kod musi zawierać co najmniej jedną cyfrę parzystą i co najmniej jedną cyfrę nieparzystą.
Ile jest kodów spełniających powyższe warunki?
Sprzedawca zegarków kupił w hurtowni za 5746 złotych dwa rodzaje zegarków: damskie i męskie, przy czym kupił trzy razy więcej zegarków damskich niż męskich. Przy ponownym zakupie takiej samej ilości zegarków, otrzymał 10% rabatu na cenę zakupu zegarka damskiego oraz 10 zł upustu na cenę zakupu zegarka męskiego. Dzięki otrzymanym rabatom, łączny koszt zakupu zmalał do 5265 zł. Wiedząc, że po udzieleniu rabatu, cena męskiego zegarka była dwa razy wyższa od ceny zegarka damskiego, oblicz pierwotne ceny zegarków.
Podstawą ostrosłupa 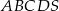 jest kwadrat
jest kwadrat 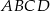 . Trójkąt równoramienny
. Trójkąt równoramienny 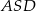 ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź
ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 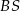 ma długość 17. Oblicz cosinus kąta nachylenia płaszczyzny
ma długość 17. Oblicz cosinus kąta nachylenia płaszczyzny 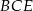 do płaszczyzny podstawy, gdzie
do płaszczyzny podstawy, gdzie 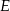 jest środkiem krawędzi
jest środkiem krawędzi 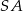 .
.
Trapez równoramienny o obwodzie 20 dm i przekątnej długości 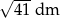 jest opisany na okręgu. Oblicz jego pole i cosinusy jego kątów wewnętrznych.
jest opisany na okręgu. Oblicz jego pole i cosinusy jego kątów wewnętrznych.

