/Szkoła średnia/Zadania maturalne
Poprawkowy Egzamin Maturalny
z Matematyki poziom podstawowy 23 sierpnia 2010 Czas pracy: 170 minut
Zadania zamknięte
Cena towaru bez podatku VAT jest równa 60 zł. Towar ten wraz z podatkiem VAT w wysokości 22% kosztuje
A) 73,20 zł B) 49,18 zł C) 60,22 zł D) 82 zł
Iloczyn 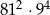 jest równy
jest równy
A) 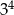 B)
B) 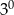 C)
C) 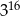 D)
D) 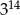
Różnica 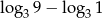 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej.
![]()
A) 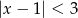 B)
B) 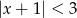 C)
C) 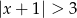 D)
D) 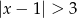
Wyrażenie 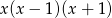 jest równe
jest równe
A) 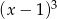 B)
B) 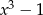 C)
C) 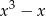 D)
D) 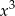
Kwadrat liczby 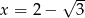 jest równy
jest równy
A) 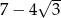 B)
B) 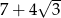 C) 1 D) 7
C) 1 D) 7
Zbiorem rozwiązań nierówności 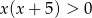 jest
jest
A) 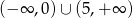
B) 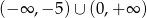
C) 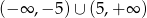
D) 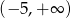
Równanie 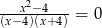
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie cztery rozwiązania.
Wierzchołek paraboli 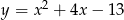 leży na prostej o równaniu
leży na prostej o równaniu
A) 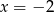 B)
B) 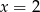 C)
C) 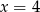 D)
D) 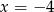
Wskaż 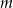 , dla którego funkcja liniowa
, dla którego funkcja liniowa 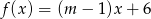 jest rosnąca
jest rosnąca
A) 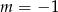 B)
B) 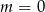 C)
C) 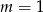 D)
D) 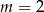
Zbiorem wartości funkcji kwadratowej 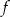 jest przedział
jest przedział 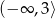 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 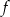 ?
?
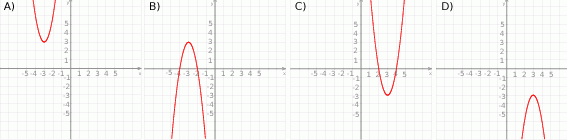
Na którym rysunku przedstawiono wykres funkcji liniowej 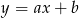 takiej, że
takiej, że 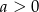 i
i  ?
?
Do wykresu funkcji 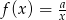 , dla
, dla 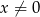 należy punkt
należy punkt 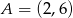 . Wtedy
. Wtedy
A) 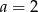 B)
B) 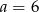 C)
C) 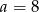 D)
D) 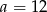
W ciągu arytmetycznym 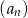 mamy:
mamy: 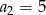 i
i 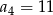 . Oblicz
. Oblicz 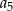 .
.
A) 8 B) 14 C) 17 D) 6
W malejącym ciągu geometrycznym 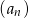 mamy:
mamy: 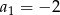 i
i 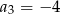 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -2 B) 2 C) 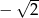 D)
D) 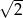
Kąt  jest ostry i
jest ostry i 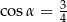 . Wtedy
. Wtedy 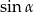 jest równy
jest równy
A) 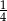 B)
B) 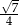 C)
C) 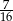 D)
D) 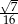
Okrąg opisany na trójkącie równobocznym ma promień równy 12. Wysokość tego trójkąta jest równa
A) 18 B) 20 C) 22 D) 24
Przekątna 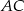 prostokąta
prostokąta 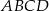 ma długość 11, a bok
ma długość 11, a bok 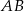 jest od niej o 5 krótszy. Oblicz długość boku
jest od niej o 5 krótszy. Oblicz długość boku 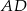 .
.
A) 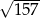 B)
B) 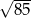 C) 5 D)
C) 5 D) 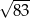
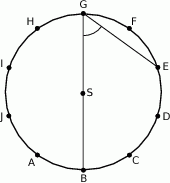
Punkty 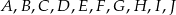 dzielą okrąg o środku
dzielą okrąg o środku 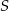 na 10 równych łuków. Oblicz miarę kąta wpisanego
na 10 równych łuków. Oblicz miarę kąta wpisanego 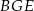 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 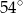 B)
B) 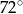 C)
C) 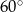 D)
D) 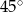
Punkty 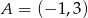 i
i 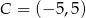 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 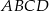 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 10 B) 25 C) 50 D) 100
Promień okręgu o równaniu 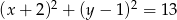 jest równy
jest równy
A) 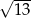 B) 13 C) 8 D)
B) 13 C) 8 D) 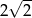
Prosta 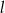 ma równanie
ma równanie 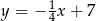 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 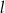 .
.
A) 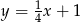 B)
B) 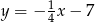 C)
C) 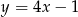 D)
D) 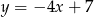
Objętość sześcianu jest równa 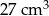 . Jaka jest suma długości wszystkich krawędzi tego sześcianu?
. Jaka jest suma długości wszystkich krawędzi tego sześcianu?
A) 18 cm B) 36 cm C) 24 cm D) 12 cm
Graniastosłup ma 15 krawędzi. Ile wierzchołków ma ten graniastosłup?
A) 10 B) 5 C) 15 D) 30
Ze zbioru liczb 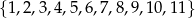 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 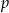 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 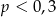 B)
B) 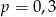 C)
C) 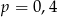 D)
D) 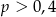
Zadania otwarte
Rozwiąż nierówność: 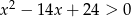 .
.
Rozwiąż równanie 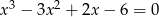 .
.
Piąty wyraz ciągu arytmetycznego jest równy 26, a suma pięciu początkowych wyrazów tego ciągu jest równa 70. Oblicz pierwszy wyraz tego ciągu.
Wyznacz równanie okręgu o środku 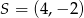 przechodzącego przez punkt
przechodzącego przez punkt 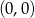 .
.
Wykaż, że trójkąt o wierzchołkach 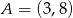 ,
, 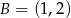 ,
, 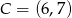 jest prostokątny.
jest prostokątny.
Wykaż, że jeżeli 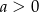 i
i 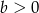 oraz
oraz 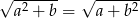 , to
, to 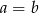 lub
lub 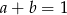 .
.
Rzucamy dwukrotnie sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma liczb oczek otrzymanych na obu kostkach jest większa od 6 i iloczyn tych liczb jest nieparzysty.
Dany jest graniastosłup prawidłowy trójkątny 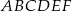 o podstawach
o podstawach 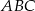 i
i 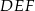 i krawędziach bocznych
i krawędziach bocznych 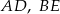 i
i 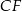 . Oblicz pole trójkąta
. Oblicz pole trójkąta 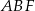 wiedząc, że
wiedząc, że 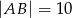 i
i 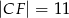 . Narysuj ten graniastosłup i zaznacz na nim trójkąt
. Narysuj ten graniastosłup i zaznacz na nim trójkąt 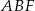 .
.
Kolarz przejechał trasę długości 60 km. Gdyby jechał ze średnią prędkością większą o 1 km/h, to przejechałby tę trasę w czasie o 6 minut krótszym. Oblicz, z jaką średnią prędkością jechał ten kolarz.

