/Szkoła średnia/Zadania maturalne

Egzamin Maturalny
z Matematyki poziom rozszerzony
(technikum) 8 maja 2015 Czas pracy: 180 minut

Zadanie 1
(3 pkt)

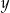Wykaż, że dla każdej dodatniej liczby rzeczywistej x różnej od 1 oraz dla każdej dodatniej liczby rzeczywistej y różnej od 1 prawdziwa jest równość

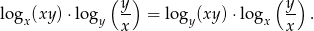
( ) ( ) log (xy) ⋅lo g y- = log (xy )⋅log y- . x y x y x x

Zadanie 2
(5 pkt)

Dany jest wielomian 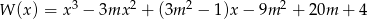3 2 2 2 W (x) = x − 3mx + (3m − 1)x− 9m + 20m + 4 . Wykres tego wielomianu, po przesunięciu o wektor →u = [− 3,0] , przechodzi przez początek układu współrzędnych. Wyznacz wszystkie pierwiastki wielomianu 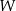W .

Zadanie 3
(6 pkt)

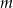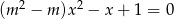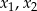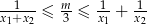Wyznacz wszystkie wartości parametru m , dla których równanie (m 2 − m)x 2 − x + 1 = 0 ma dwa różne rozwiązania rzeczywiste x1,x2 takie, że --1-- m- 1- 1- x1+x2 ≤ 3 ≤ x1 + x2 .

Zadanie 4
(6 pkt)

Trzy liczby tworzą ciąg arytmetyczny. Jeśli do pierwszej z nich dodamy 5, do drugiej 3, a do trzeciej 4, to otrzymamy rosnący ciąg geometryczny, w którym trzeci wyraz jest cztery razy większy od pierwszego. Znajdź te liczby.

Zadanie 5
(4 pkt)

Rozwiąż równanie 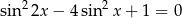sin22x − 4 sin2x + 1 = 0 w przedziale ⟨0 ,2π⟩ .

Zadanie 6
(4 pkt)

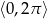Rozwiąż nierówność 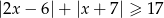|2x − 6|+ |x+ 7| ≥ 17 .

Zadanie 7
(4 pkt)

O trapezie 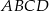ABCD wiadomo, że można w niego wpisać okrąg, a ponadto długości jego boków 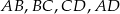AB ,BC ,CD ,AD – w podanej kolejności – tworzą ciąg geometryczny. Uzasadnij, że trapez 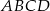ABCD jest rombem.

Zadanie 8
(4 pkt)

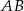Na boku AB trójkąta równobocznego 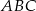ABC wybrano punkt 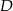D taki, że 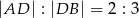|AD | : |DB | = 2 : 3 . Oblicz tangens kąta ACD .

Zadanie 9
(5 pkt)

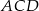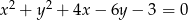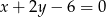Wyznacz równania prostych stycznych do okręgu o równaniu x 2 + y 2 + 4x − 6y− 3 = 0 i zarazem prostopadłych do prostej x + 2y − 6 = 0 .

Zadanie 10
(6 pkt)

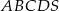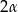Krawędź podstawy ostrosłupa prawidłowego czworokątnego ABCDS ma długość a . Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem 2α . Ostrosłup ten przecięto płaszczyzną, która przechodzi przez krawędź podstawy i dzieli na połowy kąt pomiędzy ścianą boczną i podstawą. Oblicz pole powstałego przekroju tego ostrosłupa.

Zadanie 11
(3 pkt)

Rozważmy rzut sześcioma kostkami do gry, z których każda ma inny kolor. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że uzyskany wynik rzutu spełnia równocześnie trzy warunki:
– dokładnie na dwóch kostkach otrzymano po jednym oczku;
– dokładnie na trzech kostkach otrzymano po sześć oczek;
– suma wszystkich otrzymanych liczb oczek jest parzysta.

Arkusz Wersja PDF
Rozwiązania