/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki poziom podstawowy 5 maja 2021 Czas pracy: 170 minut
Zadania zamknięte
Liczba 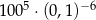 jest równa
jest równa
A) 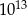 B)
B) 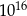 C)
C) 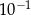 D)
D) 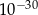
Liczba 78 stanowi 150% liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 60 B) 52 C) 48 D) 39
Rozważamy przedziały liczbowe 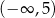 i
i 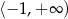 . Ile jest wszystkich liczb całkowitych, które należą jednocześnie do obu rozważanych przedziałów?
. Ile jest wszystkich liczb całkowitych, które należą jednocześnie do obu rozważanych przedziałów?
A) 6 B) 5 C) 4 D) 7
Suma 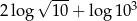 jest równa
jest równa
A) 2 B) 3 C) 4 D) 5
Różnica 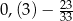 jest równa
jest równa
A) 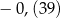 B)
B) 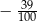 C)
C) 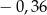 D)
D) 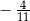
Zbiorem wszystkich rozwiązań nierówności 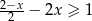 jest przedział
jest przedział
A) 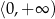 B)
B) 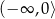 C)
C) 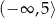 D)
D) 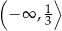
Na poniższym rysunku przedstawiono wykres funkcji 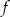 określonej w zbiorze
określonej w zbiorze 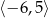 .
.
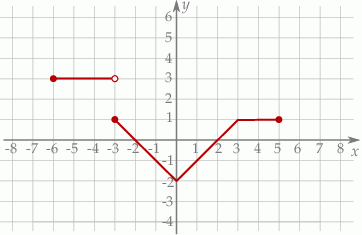
Funkcja 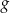 jest określona wzorem
jest określona wzorem 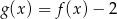 dla
dla 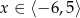 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Liczba 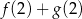 jest równa
jest równa 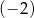 .
.
B) Zbiory wartości funkcji 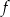 i
i 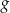 są równe.
są równe.
C) Funkcje 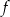 i
i 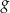 mają te same miejsca zerowe.
mają te same miejsca zerowe.
D) Punkt 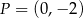 należy do wykresów funkcji
należy do wykresów funkcji 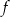 i
i 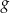 .
.
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
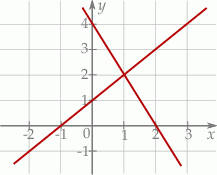
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 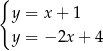 B)
B) 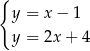 C)
C) 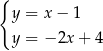 D)
D) 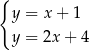
Proste o równaniach 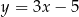 oraz
oraz 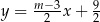 są równoległe, gdy
są równoległe, gdy
A) 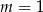 B)
B) 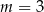 C)
C) 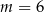 D)
D) 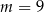
Funkcja 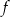 jest określona wzorem
jest określona wzorem 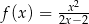 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 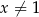 . Wtedy dla argumentu
. Wtedy dla argumentu 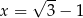 wartość funkcji
wartość funkcji 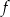 jest równa
jest równa
A) 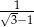 B)
B) 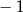 C) 1 D)
C) 1 D) 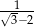
Do wykresu funkcji 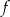 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  wzorem
wzorem 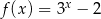 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 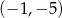 B)
B) 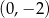 C)
C) 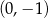 D)
D) 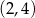
Funkcja kwadratowa 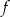 określona jest wzorem
określona jest wzorem 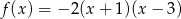 jest malejąca w przedziale
jest malejąca w przedziale
A) 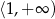 B)
B) 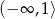 C)
C) 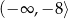 D)
D) 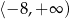
Trzywyrazowy ciąg 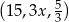 jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
A) 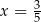 B)
B) 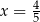 C)
C) 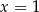 D)
D) 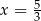
Ciąg 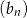 jest określony wzorem
jest określony wzorem 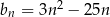 dla każdej liczby naturalnej
dla każdej liczby naturalnej 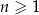 . Liczba niedodatnich wyrazów ciągu
. Liczba niedodatnich wyrazów ciągu 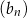 jest równa
jest równa
A) 14 B) 13 C) 9 D) 8
Ciąg arytmetyczny 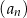 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 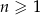 . Trzeci i piąty wyraz ciągu spełniają warunek
. Trzeci i piąty wyraz ciągu spełniają warunek 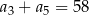 . Wtedy czwarty wyraz tego ciągu jest równy
. Wtedy czwarty wyraz tego ciągu jest równy
A) 28 B) 29 C) 33 D) 40
Dla każdego kąta ostrego  iloczyn
iloczyn 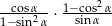 jest równy
jest równy
A) 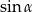 B)
B) 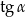 C)
C) 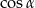 D)
D) 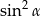
Prosta 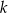 jest styczna w punkcie
jest styczna w punkcie 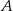 do okręgu o środku
do okręgu o środku 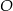 . Punkt
. Punkt 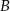 leży na tym okręgu i miara kąta
leży na tym okręgu i miara kąta 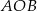 jest równa
jest równa 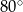 . Przez punkty
. Przez punkty 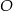 i
i 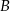 poprowadzono prostą, która przecina prostą
poprowadzono prostą, która przecina prostą 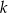 w punkcie
w punkcie 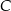 (zobacz rysunek).
(zobacz rysunek).

Miara kąta 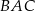 jest równa
jest równa
A) 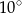 B)
B) 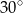 C)
C) 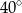 D)
D) 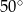
Przyprostokątna 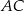 trójkąta prostokątnego
trójkąta prostokątnego 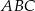 ma długość 8 oraz
ma długość 8 oraz 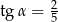 (zobacz rysunek).
(zobacz rysunek).
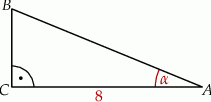
Pole tego trójkąta jest równe
A) 12 B) 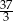 C)
C) 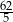 D)
D) 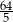
Pole pewnego trójkąta równobocznego jest równe 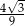 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 4 B) 2 C) 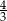 D)
D) 
W trójkącie 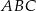 bok
bok 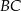 ma długość 13, a wysokość
ma długość 13, a wysokość 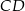 tego trójkąta dzieli bok
tego trójkąta dzieli bok 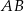 na odcinki o długościach
na odcinki o długościach 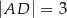 i
i 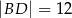 (zobacz rysunek obok).
(zobacz rysunek obok).
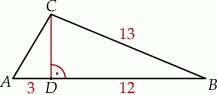
Długość boku 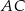 jest równa
jest równa
A) 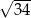 B)
B) 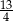 C)
C) 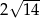 D)
D) 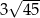
Punkty 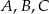 i
i 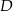 leżą na okręgu o środku
leżą na okręgu o środku 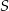 . Miary kątów
. Miary kątów 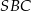 ,
, 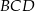 ,
, 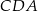 są równe odpowiednio:
są równe odpowiednio: 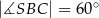 ,
, 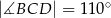 ,
, 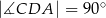 (zobacz rysunek).
(zobacz rysunek).
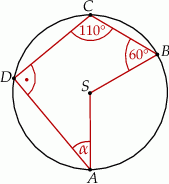
Wynika stąd, że miara  kąta
kąta 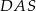 jest równa
jest równa
A) 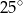 B)
B) 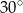 C)
C) 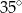 D)
D) 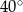
W równoległoboku 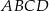 , przedstawionym na rysunku, kąt
, przedstawionym na rysunku, kąt  ma miarę
ma miarę 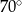 .
.
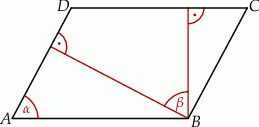
Wtedy kąt 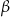 ma miarę
ma miarę
A) 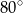 B)
B) 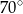 C)
C) 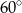 D)
D) 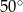
W każdym  –kącie wypukłym (
–kącie wypukłym (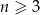 ) liczba przekątnych jest równa
) liczba przekątnych jest równa 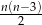 . Wielokątem wypukłym, w którym liczba przekątnych jest o 25 większa od liczby boków, jest
. Wielokątem wypukłym, w którym liczba przekątnych jest o 25 większa od liczby boków, jest
A) siedmiokąt. B) dziesięciokąt. C) dwunastokąt. D) piętnastokąt.
Pole figury 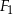 złożonej z dwóch stycznych zewnętrznie kół o promieniach 1 i 3 jest równe polu figury
złożonej z dwóch stycznych zewnętrznie kół o promieniach 1 i 3 jest równe polu figury 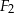 złożonej z dwóch stycznych zewnętrznie kół o promieniach długości
złożonej z dwóch stycznych zewnętrznie kół o promieniach długości  (zobacz rysunek).
(zobacz rysunek).
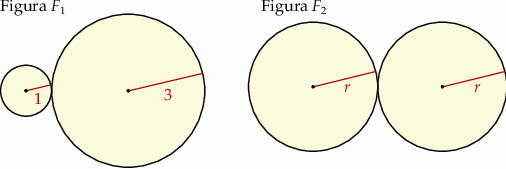
Długość  promienia jest równa
promienia jest równa
A) 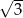 B) 2 C)
B) 2 C) 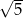 D) 3
D) 3
Punkt 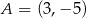 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 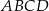 , a punkt
, a punkt 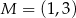 jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu
jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu 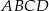 jest równe
jest równe
A) 68 B) 136 C) 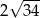 D)
D) 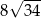
Z wierzchołków sześcianu 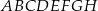 losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu
losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu 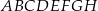 , jest równe
, jest równe
A) 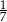 B)
B) 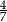 C)
C) 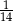 D)
D) 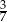
Wszystkich liczb naturalnych trzycyfrowych, większych od 700, w których każda cyfra należy do zbioru 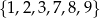 i żadna cyfra się nie powtarza, jest
i żadna cyfra się nie powtarza, jest
A) 108 B) 60 C) 40 D) 299
Sześciowyrazowy ciąg liczbowy 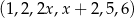 jest niemalejący. Mediana wyrazów tego ciągu jest równa 4. Wynika stąd, że
jest niemalejący. Mediana wyrazów tego ciągu jest równa 4. Wynika stąd, że
A) 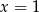 B)
B) 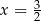 C)
C) 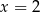 D)
D) 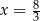
Zadania otwarte
Rozwiąż nierówność 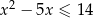 .
.
Wykaż, że dla każdych trzech dodatnich liczb 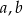 i
i  takich, że
takich, że 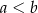 , spełniona jest nierówność
, spełniona jest nierówność
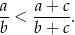
Funkcja liniowa 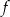 przyjmuje wartość 2 dla argumentu 0, a ponadto
przyjmuje wartość 2 dla argumentu 0, a ponadto 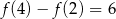 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 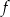 .
.
Rozwiąż równanie
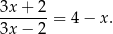
Trójkąt równoboczny 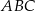 ma pole równe
ma pole równe 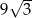 . Prosta równoległa do boku
. Prosta równoległa do boku 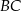 przecina boki
przecina boki 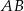 i
i 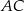 – odpowiednio – w punktach
– odpowiednio – w punktach 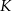 i
i 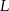 . Trójkąty
. Trójkąty 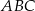 i
i 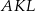 są podobne, a stosunek długości boków tych trójkątów jest równy
są podobne, a stosunek długości boków tych trójkątów jest równy  . Oblicz długość boku trójkąta
. Oblicz długość boku trójkąta 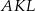 .
.
Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza sumę liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia 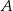 polegającego na tym, że suma liczb wyrzuconych oczek jest równa 4 lub 5, lub 6.
polegającego na tym, że suma liczb wyrzuconych oczek jest równa 4 lub 5, lub 6.
Punkty 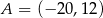 i
i 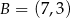 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 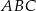 , w którym
, w którym 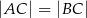 . Wierzchołek
. Wierzchołek 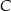 leży na osi
leży na osi 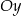 układu współrzędnych. Oblicz współrzędne wierzchołka
układu współrzędnych. Oblicz współrzędne wierzchołka 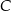 oraz obwód tego trójkąta.
oraz obwód tego trójkąta.

