/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 7 kwietnia 2018 Czas pracy: 180 minut
Zadania zamknięte
Wskaż liczbę, która spełnia równanie 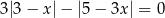
A) 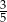 B)
B) 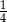 C)
C) 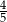 D)
D) 
Liczba 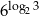 jest równa
jest równa
A) 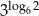 B)
B) 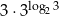 C)
C) 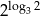 D)
D) 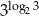
Okrąg jest styczny do boku 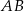 trójkąta
trójkąta 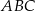 w punkcie
w punkcie 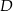 oraz przecina boki
oraz przecina boki 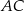 i
i 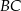 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 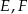 i
i 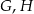 (zobacz rysunek). Kat
(zobacz rysunek). Kat 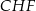 ma miarę
ma miarę 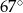 .
.
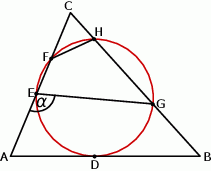
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 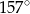 B)
B) 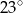 C)
C) 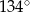 D)
D) 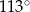
Wskaż liczbę spełniającą nierówność 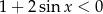 .
.
A) 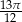 B)
B) 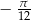 C)
C) 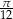 D)
D) 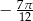
Ciąg 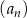 określony jest w następujący sposób
określony jest w następujący sposób 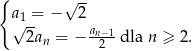 Setny wyraz ciągu
Setny wyraz ciągu 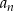 jest równy
jest równy
A) 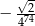 B)
B) 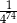 C)
C) 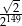 D)
D) 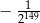
Zadania otwarte
Funkcja kwadratowa 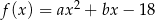 ma dwa miejsca zerowe:
ma dwa miejsca zerowe: 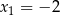 i
i 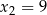 . Oblicz najmniejszą wartość tej funkcji.
. Oblicz najmniejszą wartość tej funkcji.
Oblicz granicę 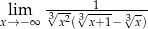 .
.
W trójkącie ostrokątnym 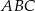 bok
bok 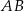 ma długość
ma długość  , długość boku
, długość boku 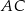 jest równa
jest równa 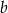 oraz
oraz 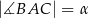 . Dwusieczna kąta
. Dwusieczna kąta 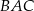 przecina bok
przecina bok 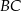 trójkąta w punkcie
trójkąta w punkcie 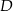 i odcinek
i odcinek 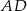 ma długość
ma długość 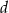 . Wykaż, że
. Wykaż, że
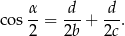
Prosta o równaniu 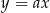 przecina parabolę o równaniu
przecina parabolę o równaniu 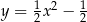 w dwóch punktach
w dwóch punktach 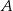 i
i 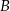 . Wykaż, że styczne do tej paraboli w punktach
. Wykaż, że styczne do tej paraboli w punktach 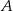 i
i 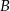 są prostopadłe.
są prostopadłe.
Na loterii jest 20 losów, wśród których jeden los wygrywa 600 zł, pięć losów wygrywa po 200 zł i sześć losów wygrywa po 150 zł. Pozostałe losy są przegrywające. Jakie jest prawdopodobieństwo tego, że kupując jako pierwsi cztery razy po jednym losie wygramy dokładnie 600 zł?
Rozwiąż równanie 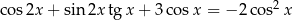 w przedziale
w przedziale 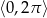 .
.
Ciąg 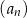 jest ciągiem arytmetycznym o pierwszym wyrazie równym 123 i różnicy będącej liczbą całkowitą. Ciąg
jest ciągiem arytmetycznym o pierwszym wyrazie równym 123 i różnicy będącej liczbą całkowitą. Ciąg 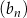 jest określony wzorem
jest określony wzorem 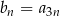 , dla
, dla 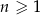 , oraz wiadomo, że suma pewnych
, oraz wiadomo, że suma pewnych 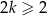 początkowych wyrazów ciągu
początkowych wyrazów ciągu 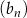 jest równa sumie
jest równa sumie 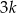 początkowych wyrazów ciągu
początkowych wyrazów ciągu 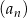 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 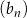 .
.
W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez krawędź podstawy oraz przez środek symetrii graniastosłupa. Płaszczyzna ta wyznacza przekrój o polu równym 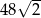 . Stosunek wysokości graniastosłupa do długości krawędzi podstawy jest równy
. Stosunek wysokości graniastosłupa do długości krawędzi podstawy jest równy 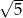 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Trapez równoramienny 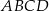 o ramieniu długości 7 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 7 wpisany jest w okrąg, przy czym dłuższa podstawa 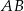 trapezu, o długości 14, jest średnicą tego okręgu. Przekątne
trapezu, o długości 14, jest średnicą tego okręgu. Przekątne 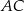 i
i 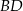 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 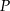 . Oblicz długość okręgu wpisanego w trójkąt
. Oblicz długość okręgu wpisanego w trójkąt 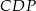 .
.
Wyznacz wszystkie wartości parametru 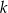 , dla których równanie
, dla których równanie
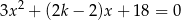
ma dwa różne rozwiązania rzeczywiste 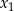 i
i 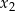 , przy czym
, przy czym 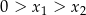 , spełniające warunek
, spełniające warunek
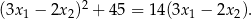
Rozpatrujemy wszystkie prostopadłościany o objętości 27, których stosunek długości dwóch krawędzi wychodzących z tego samego wierzchołka jest równy 1:3 oraz suma długości wszystkich dwunastu krawędzi jest mniejsza od 52. Wyznacz pole powierzchni całkowitej prostopadłościanu jako funkcję długości jednej z jego krawędzi. Wyznacz dziedzinę tej funkcji. Oblicz wymiary tego spośród rozpatrywanych prostopadłościanów, którego pole powierzchni całkowitej jest najmniejsze.

