/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki poziom rozszerzony 14 maja 2008 Czas pracy: 180 minut
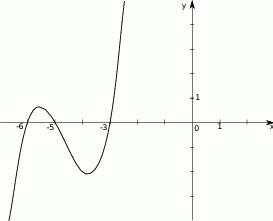
Wielomian stopnia trzeciego 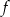 , którego fragment wykresu przedstawiono na poniższym rysunku spełnia warunek
, którego fragment wykresu przedstawiono na poniższym rysunku spełnia warunek 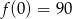 .
.
Wielomian 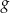 dany jest wzorem
dany jest wzorem 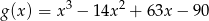 . Wykaż, że
. Wykaż, że 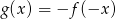 dla
dla 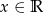 .
.
Rozwiąż nierówność 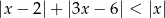 .
.
Liczby 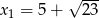 i
i 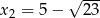 są rozwiązaniami równania
są rozwiązaniami równania 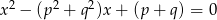 z niewiadomą
z niewiadomą  . Oblicz wartości
. Oblicz wartości 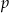 i
i 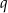 .
.
Rozwiąż równanie 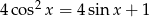 w przedziale
w przedziale 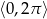 .
.
Dane jest równanie 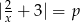 z niewiadomą
z niewiadomą  . Wyznacz liczbę rozwiązań tego równania w zależności od parametru
. Wyznacz liczbę rozwiązań tego równania w zależności od parametru 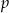 .
.
Udowodnij, że jeżeli ciąg 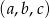 jest jednocześnie arytmetyczny i geometryczny to
jest jednocześnie arytmetyczny i geometryczny to 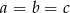 .
.
Udowodnij, że każdy punkt paraboli o równaniu 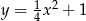 jest równoodległy od osi
jest równoodległy od osi 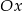 i od punktu
i od punktu 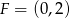 .
.
Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu 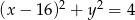 jest okrąg o równaniu
jest okrąg o równaniu 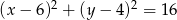 , a skala tej jednokładności jest liczbą ujemną.
, a skala tej jednokładności jest liczbą ujemną.
Wyznacz dziedzinę i najmniejszą wartość funkcji 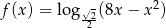 .
.
Z pewnej grupy osób, w której jest dwa razy więcej mężczyzn niż kobiet, wybrano losowo dwuosobową delegację. Prawdopodobieństwo tego, że w delegacji znajdą się tylko kobiety jest równe 0,1. Oblicz, ile kobiet i ilu mężczyzn jest w tej grupie.
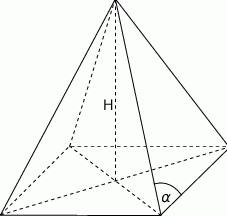
W ostrosłupie prawidłowym czworokątnym dane są: 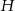 – wysokość ostrosłupa oraz
– wysokość ostrosłupa oraz  — miara kąta utworzonego przez krawędź boczną i krawędź podstawy (
— miara kąta utworzonego przez krawędź boczną i krawędź podstawy (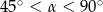 ).
).
- Wykaż, że objętość
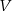 tego ostrosłupa jest równa
tego ostrosłupa jest równa 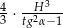 .
. - Oblicz miarę kąta
 , dla której objętość
, dla której objętość 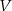 danego ostrosłupa jest równa
danego ostrosłupa jest równa 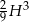 . Wynik podaj w zaookrągleniu do całkowitej liczby stopni.
. Wynik podaj w zaookrągleniu do całkowitej liczby stopni.
W trójkącie prostokątnym 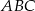 przyprostokątne mają długości:
przyprostokątne mają długości: 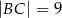 ,
, 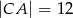 . Na boku
. Na boku 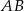 wybrano punkt
wybrano punkt 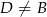 tak, że odcinki
tak, że odcinki 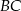 i
i 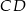 mają równe długości. Oblicz długość odcinka
mają równe długości. Oblicz długość odcinka 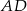 .
.

