/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 28 marca 2009 Czas pracy: 180 minut

Zadanie 1
(4 pkt)

Podaj liczbę rozwiązań równania 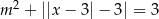2 m + ||x − 3 |− 3| = 3 w zależności od wartości parametru m .

Zadanie 2
(5 pkt)

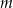Dany jest trójkąt o bokach długości 7,8,9.

  • Oblicz promień okręgu wpisanego w ten trójkąt.
  • Oblicz sumę sinusów kątów tego trójkąta.

Zadanie 3
(5 pkt)

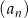Ciąg (an) dany jest wzorem 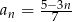an = 5−73n- , dla n ≥ 1 .

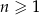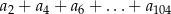  • Oblicz sumę a2 + a4 + a6 + ...+ a104 .
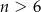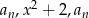  • Ustalmy n > 6 . Dla jakich x liczby 2 an ,x + 2,an są kolejnymi wyrazami ciągu geometrycznego?

Zadanie 4
(5 pkt)

Wiedząc, że wielomian 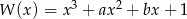W (x) = x3 + ax2 + bx + 1 jest podzielny przez wielomian 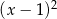(x − 1)2 , oblicz a i b .

Zadanie 5
(5 pkt)

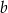W urnie znajdują się kule czarne, białe i niebieskie, przy czym są co najmniej dwie kule każdego koloru i w sumie jest 15 kul. Losujemy z urny trzy kule. Rozważmy następujące zdarzenia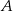
A – wylosowano trzy kule tego samego koloru;
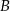B – żadne dwie z wylosowanych kul nie są tego samego koloru.
Oblicz prawdopodobieństwo zdarzenia 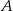A jeżeli prawdopodobieństwo zdarzenia 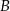B jest równe -3 13 .

Zadanie 6
(5 pkt)

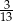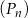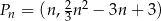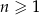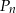Dany jest ciąg punktów (Pn) na płaszczyźnie, których współrzędne dane są wzorem Pn = (n, 2n 2 − 3n + 3) 3 , gdzie n ≥ 1 . Wyznacz tę wartość n , dla której odległość punktu P n od prostej 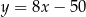y = 8x − 50 jest najmniejsza z możliwych.

Zadanie 7
(4 pkt)

Dwa samochody odbyły podróż z miejscowości 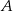A do odległej o 480 km miejscowości 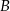B . Drugi z samochodów jechał ze średnią prędkością większą o 20 km/h od średniej prędkości pierwszego samochodu, a czas przejazdu pierwszego samochodu był o 72 minuty dłuższy od czasu przejazdu drugiego samochodu. Oblicz ile czasu zajęła podróż każdemu z samochodów.

Zadanie 8
(4 pkt)

Podstawa trójkąta równoramiennego ma długość 4. Środek okręgu opisanego na tym trójkącie dzieli jedną z wysokości trójkąta na odcinki, których stosunek długości wynosi 3:5. Oblicz długość ramienia trójkąta.

Zadanie 9
(5 pkt)

Wykres funkcji 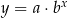x y = a⋅ b powstaje z wykresu funkcji 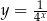1- y = 4x przez jednokładność o środku w punkcie 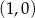(1,0) i skali 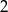2 . Wyznacz liczby a i b .

Zadanie 10
(4 pkt)

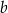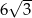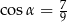Podstawą graniastosłupa prawidłowego jest trójkąt, w którym wysokość ma długość √ -- 6 3 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt α taki, że cosα = 7 9 . Oblicz objętość graniastosłupa.

Zadanie 11
(4 pkt)

Suma dwóch liczb jest równa 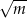√ -- m , a ich różnica jest równa 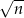√ -- n , gdzie 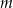m i n są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.

Arkusz Wersja PDF
Rozwiązania