/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy
(technikum) 18 kwietnia 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 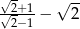 jest liczbą
jest liczbą
A) wymierną B) niewymierną C) mniejszą niż 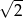 D) naturalną
D) naturalną
Liczba osób planujących wziąć udział w demonstracji początkowo wzrosła o 20%, a po dwóch dniach zmalała o 30%. W wyniku tych dwóch zmian liczba osób planujących wziąć udział w demonstracji zmalała o
A) 16% B) 10% C) 56% D) 84%
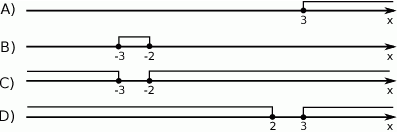
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 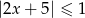 .
.
Wielomian 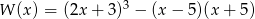 przedstawiony w postaci sumy algebraicznej przyjmuje postać:
przedstawiony w postaci sumy algebraicznej przyjmuje postać:
A) 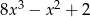 B)
B) 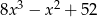 C)
C) 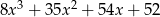 D)
D) 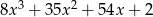
Układ równań 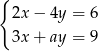 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 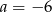 B)
B) 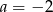 C)
C) 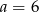 D)
D) 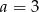
Dla każdego kąta ostrego  wyrażenie
wyrażenie 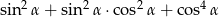 jest równe
jest równe
A) 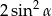 B)
B) 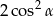 C) 1 D) 2
C) 1 D) 2
Pole działki budowlanej jest równe 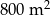 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 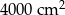 B)
B) 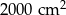 C)
C) 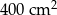 D)
D) 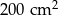
Liczba 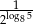 jest równa
jest równa
A) 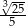 B)
B) 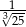 C)
C) 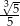 D)
D) 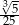
Równanie 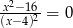
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie cztery rozwiązania.
Liczby 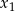 i
i 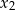 są pierwiastkami równania
są pierwiastkami równania 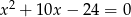 i
i 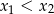 . Oblicz
. Oblicz 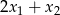 .
.
A) -22 B) -17 C) 8 D) 13
Która z liczb jest największa?
A) 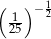 B)
B) 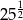 C)
C) 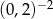 D)
D) 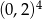
Punkt 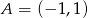 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 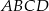 , którego bok
, którego bok 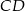 zawiera się w prostej
zawiera się w prostej 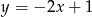 . Podstawa
. Podstawa 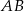 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 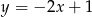 B)
B) 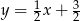 C)
C) 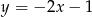 D)
D) 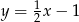
Stopień wielomianu 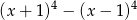 jest równy
jest równy
A) 4 B) 3 C) 2 D) 1
W malejącym ciągu geometrycznym 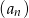 mamy:
mamy: 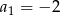 i
i 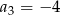 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -2 B) 2 C) 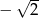 D)
D) 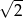
Punkt 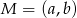 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 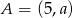 i
i 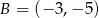 . Wówczas
. Wówczas
A) 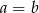 B)
B) 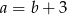 C)
C) 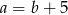 D)
D) 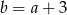
Podstawa trójkąta równoramiennego ma długość 10, a ramię ma długość 13. Wysokość opuszczona na podstawę ma długość
A) 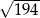 B)
B) 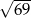 C) 12 D) 11
C) 12 D) 11
Dana jest parabola o równaniu 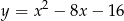 . Pierwsza współrzędna wierzchołka tej paraboli jest równa
. Pierwsza współrzędna wierzchołka tej paraboli jest równa
A) 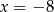 B)
B) 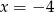 C)
C) 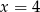 D)
D) 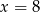
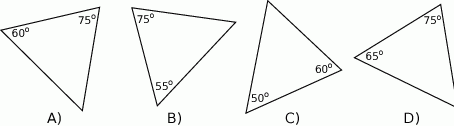
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 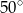 i
i 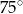 ?
?
Objętość walca o wysokości 4 jest równa 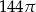 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 9 B) 8 C) 6 D) 3
W prostopadłościanie 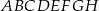 mamy:
mamy: 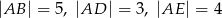 . Który z odcinków
. Który z odcinków 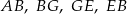 jest najdłuższy?
jest najdłuższy?
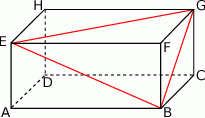
A) 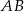 B)
B) 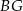 C)
C) 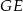 D)
D) 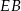
Funkcja
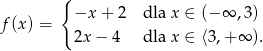
A) nie ma miejsc zerowych
B) ma dwa miejsca zerowe
C) ma jedno miejsce zerowe
D) ma trzy miejsca zerowe
Pewna firma zatrudnia 7 osób. Dyrektor zarabia 7000 zł, a pensje pozostałych pracowników są równe: 4200 zł, 2800 zł, 2600 zł, 3400 zł, 3600 zł, 3000 zł. Mediana zarobków tych 7 osób jest równa
A) 3400 zł B) 3500 zł C) 3200 zł D) 7000 zł
Zadania otwarte
Dwaj rowerzyści pokonują trasę między punktami 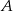 i
i 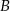 . O ile procent średnia prędkość drugiego rowerzysty musi być większa od średniej prędkości pierwszego rowerzysty, aby przyjechał on o 20% szybciej?
. O ile procent średnia prędkość drugiego rowerzysty musi być większa od średniej prędkości pierwszego rowerzysty, aby przyjechał on o 20% szybciej?
Kąt  jest ostry i
jest ostry i 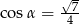 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 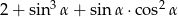 .
.
Wykaż, że jeżeli przy dzieleniu przez 5 jedna liczba daję resztę 2, a druga resztę 3, to iloczyn tych liczb daje przy dzieleniu przez 5 resztę 1.
Suma  początkowych wyrazów ciągu geometrycznego
początkowych wyrazów ciągu geometrycznego 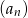 wyraża się wzorem
wyraża się wzorem 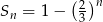 dla
dla 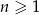 . Oblicz pierwszy wyraz ciągu i jego iloraz.
. Oblicz pierwszy wyraz ciągu i jego iloraz.
Dany jest trójkąt równoboczny 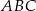 . Okrąg o średnicy
. Okrąg o średnicy 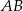 przecina bok
przecina bok 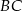 w punkcie
w punkcie 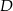 .
.
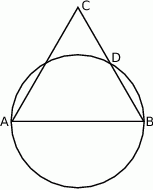
Wykaż, że 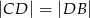 .
.
Rozwiąż równanie 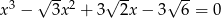 .
.
Wyznacz równania stycznych do okręgu o równaniu 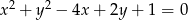 , równoległych do osi odciętych układu współrzędnych.
, równoległych do osi odciętych układu współrzędnych.
Prosta równoległa do jednego boku trójkąta dzieli jego pole na połowy. W jakim stosunku prosta ta dzieli pozostałe boki trójkąta?
Dany jest graniastosłup prawidłowy trójkątny 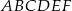 o podstawach
o podstawach 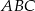 i
i 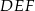 i krawędziach bocznych
i krawędziach bocznych 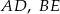 i
i 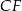 . Oblicz pole trójkąta
. Oblicz pole trójkąta 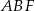 wiedząc, że
wiedząc, że 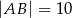 i
i 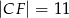 . Narysuj ten graniastosłup i zaznacz na nim trójkąt
. Narysuj ten graniastosłup i zaznacz na nim trójkąt 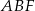 .
.
W pojemniku umieszczono 50 drewnianych klocków, przy czym każdy klocek ma kształt sześcianu lub kuli, oraz każdy klocek jest czerwony lub niebieski. Wiadomo, że w pojemniku znajduje się dokładnie 15 czerwonych sześcianów, 18 klocków niebieskich i 31 klocków mających kształt kuli. Z pojemnika losowo wybieramy jeden klocek. Oblicz prawdopodobieństwo, że wylosowany klocek jest niebieską kulą.

