/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 3 marca 2012 Czas pracy: 180 minut
Wyznacz w zależności od parametru 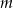 liczbę rozwiązań równania
liczbę rozwiązań równania 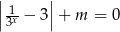 .
.
Udowodnij, że liczba 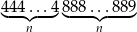 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Punkt 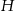 jest punktem wspólnym wysokości trójkąta ostrokątnego
jest punktem wspólnym wysokości trójkąta ostrokątnego 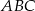 wpisanego w okrąg o promieniu 12. Oblicz promień okręgu opisanego na trójkącie
wpisanego w okrąg o promieniu 12. Oblicz promień okręgu opisanego na trójkącie 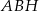 .
.
Wyznacz wszystkie liczby 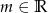 , dla których równanie
, dla których równanie 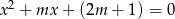 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 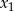 i
i 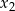 takie, że
takie, że 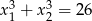 .
.
Oblicz sumę wszystkich liczb czterocyfrowych, które przy dzieleniu przez 23 dają resztę 7.
Rozwiąż równanie 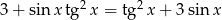 w przedziale
w przedziale 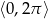 .
.
Uzasadnij, że jeżeli liczby niezerowe 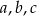 spełniają warunek
spełniają warunek 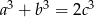 to
to
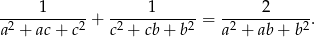
Trójkąt równoramienny o obwodzie 12 obraca się wokół swojej osi symetrii. Oblicz dla jakich długości boków trójkąta otrzymamy stożek, w którym różnica między polem powierzchni bocznej, a polem podstawy jest największa. Oblicz objętość tego stożka.
W trapezie 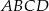 , w którym
, w którym 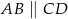 , dane są wierzchołki
, dane są wierzchołki 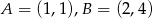 oraz punkt przecięcia przekątnych
oraz punkt przecięcia przekątnych 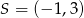 . Pole trapezu jest równe 36.
. Pole trapezu jest równe 36.
- Oblicz długość podstawy
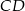 .
. - Wyznacz współrzędne wierzchołków
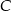 i
i 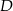 .
.
Danych jest 5 pudełek ponumerowanych liczbami od 1 do 5. W każdym pudełku znajduje się 20 kul ponumerowanych liczbami od 1 do 20. Z każdego pudełka wybieramy jedną kulę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że każda z wylosowanych liczb jest mniejsza od wszystkich liczb wylosowanych z pudełek o większych numerach. Wynik podaj w postaci ułamka nieskracalnego.
Podstawą ostrosłupa jest trójkąt równoramienny o ramieniu długości 10 i podstawie długości 12. Wszystkie krawędzie boczne ostrosłupa mają długość 7. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.

