/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy+ 30 kwietnia 2011 Czas pracy: 170 minut
Zadania zamknięte
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 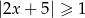 .
.
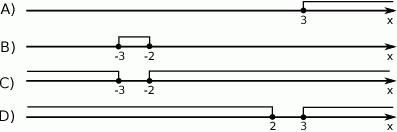
Połowa liczby  jest o 25% mniejsza od trzeciej części liczby
jest o 25% mniejsza od trzeciej części liczby  . Wtedy liczba
. Wtedy liczba  jest
jest
A) o 200% większa od 
B) o 100% większa od 
C) o 50% większa od 
D) o 150% większa od 
Iloraz 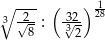 jest równy
jest równy
A) 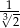 B)
B) 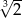 C) 1 D)
C) 1 D) 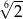
Wartość wyrażenia 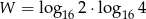 jest równa
jest równa
A) 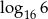 B)
B) 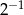 C)
C) 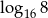 D)
D) 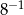
Funkcja 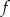 określona jest wzorem
określona jest wzorem
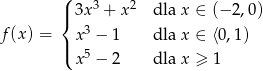
Ile miejsc zerowych ma ta funkcja?
A) 0 B) 1 C) 2 D) 3
Na diagramie przedstawione są wyniki pomiaru wzrostu uczniów pewnej klasy.
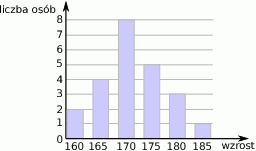
Ile osób w tej klasie ma wzrost powyżej średniego?
A) 17 B) 4 C) 21 D) 9
Przykładem liczby niewymiernej spełniającej nierówność 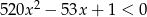 jest
jest
A) 0,04 B) 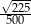 C)
C) 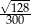 D)
D) 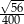
Równanie 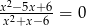
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie trzy rozwiązania
Dane są wielomiany 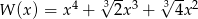 oraz
oraz 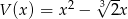 . Wielomian
. Wielomian 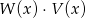 jest równy
jest równy
A) 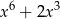 B)
B) 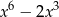 C)
C) 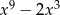 D)
D) 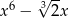
Diagram przedstawia ile procent mieszkańców pewnego osiedla było w listopadzie w kinie 0,1,2,3 lub 4 razy. Średnia liczba wyjść do kina przypadających na jednego mieszkańca jest równa
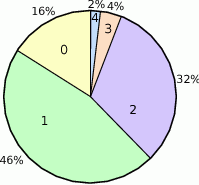
A) 1,3 B) 1,44 C) 2 D) 2,5
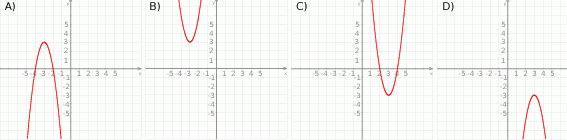
Zbiór wartości funkcji kwadratowej 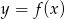 jest rozłączny z przedziałem
jest rozłączny z przedziałem 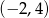 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 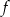 ?
?
Wskaż 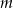 , dla którego istnieją co najmniej dwie różne liczby
, dla którego istnieją co najmniej dwie różne liczby 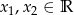 spełniające równanie
spełniające równanie 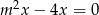 .
.
A) 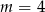 B)
B) 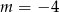 C)
C) 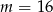 D)
D) 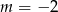
Liczba przekątnych dziewięciokąta foremnego jest równa
A) 20 B) 54 C) 21 D) 27
Pionowy słupek o wysokości 90 cm rzuca na ziemię cień. O ile procent dłuższy cień rzuca słupek o wysokości 117 cm?
A) 33,(3)% B) 13% C) 30% D) 3%
Kąt wpisany w okrąg o promieniu 12, który jest oparty na łuku długości 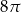 ma miarę
ma miarę
A) 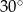 B)
B) 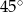 C)
C) 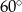 D)
D) 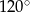
Kąt  jest ostry i
jest ostry i 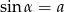 . Liczba
. Liczba  może być równa
może być równa
A) 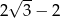 B)
B) 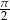 C)
C) 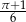 D)
D) 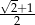
Czwarty wyraz ciągu 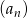 danego wzorem
danego wzorem 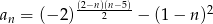 jest równy
jest równy
A) 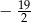 B)
B) 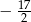 C) -11 D) 7
C) -11 D) 7
Zamawiając pizzę mamy do wyboru 12 dodatków, 2 rodzaje ciasta i 3 rodzaje sosów. Na ile sposobów możemy zamówić pizzę jeżeli zdecydowaliśmy się wybrać jeden dodatek główny i jeden dodatek pomocniczy (różny od głównego), oraz jeden sos?
A) 28 B) 792 C) 29 D) 864
Ramię trójkąta równoramiennego 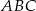 ma długość 8 cm i tworzy z podstawą kąt o mierze
ma długość 8 cm i tworzy z podstawą kąt o mierze 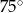 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 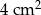 B)
B) 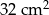 C)
C) 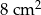 D)
D) 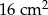
Punkty 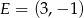 i
i 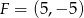 są środkami dwóch sąsiednich boków kwadratu
są środkami dwóch sąsiednich boków kwadratu 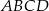 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 10 B) 25 C) 40 D) 100
Równanie okręgu wpisanego w romb o wierzchołkach 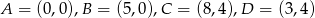 ma postać
ma postać
A) 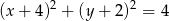
B) 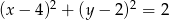
C) 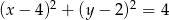
D) 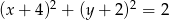
Zadania otwarte
Rozwiąż nierówność 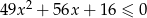 .
.
Iloraz ciągu geometrycznego 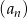 , gdzie
, gdzie 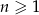 jest równy
jest równy 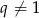 , a suma 10 początkowych wyrazów tego ciągu spełnia warunek
, a suma 10 początkowych wyrazów tego ciągu spełnia warunek 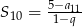 . Oblicz pierwszy wyraz tego ciągu.
. Oblicz pierwszy wyraz tego ciągu.
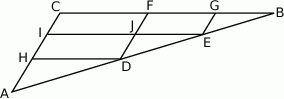
Odcinki 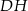 i
i 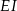 są równoległe do boku
są równoległe do boku 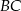 trójkąta
trójkąta 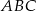 , a odcinki
, a odcinki 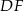 i
i 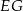 są równoległe do boku
są równoległe do boku 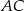 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 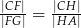 , to
, to 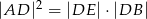 .
.
Wykaż, że jeżeli 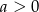 i
i 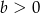 oraz
oraz 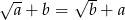 to
to 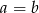 lub
lub 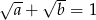 .
.
Krawędź boczna ostrosłupa prawidłowego czworokątnego jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 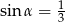 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
Wyznacz wzór na  -ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 40, a wyrazy drugi, piąty i dwudziesty trzeci tworzą w podanej kolejności ciąg geometryczny.
-ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 40, a wyrazy drugi, piąty i dwudziesty trzeci tworzą w podanej kolejności ciąg geometryczny.
W trapezie prostokątnym 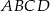 dłuższe ramię ma długość 10. Obwód tego trapezu jest równy 30. Wiedząc, że tangens kąta ostrego w trapezie
dłuższe ramię ma długość 10. Obwód tego trapezu jest równy 30. Wiedząc, że tangens kąta ostrego w trapezie 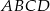 jest równy
jest równy 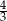 , oblicz długości jego podstaw.
, oblicz długości jego podstaw.
Punkty 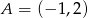 i
i 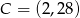 są wierzchołkami trójkąta równoramiennego, w którym
są wierzchołkami trójkąta równoramiennego, w którym 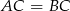 . Prosta zawierająca wysokość opuszczoną z wierzchołka
. Prosta zawierająca wysokość opuszczoną z wierzchołka 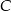 ma równanie
ma równanie 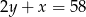 . Oblicz pole trójkąta
. Oblicz pole trójkąta 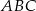 .
.

