/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki (OKE Poznań)
poziom podstawowy 11 stycznia 2010 Czas pracy: 170 minut
Zadania zamknięte
Wynikiem działania 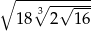 jest
jest
A) 36 B) 16 C) 12 D) 6
Połową liczby 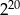 jest
jest
A) 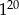 B)
B) 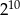 C)
C) 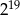 D)
D) 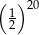
Wartość wyrażenia 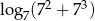 wynosi
wynosi
A) 5 B) 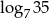 C)
C) 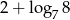 D)
D) 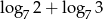
Cena towaru wzrosła z 1200 zł do 1248 zł. O jaki procent wzrosła cena?
A) 40% B) 4% C) 0,4% D) 0,04%
Najprostszą postacią wyrażenia 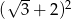 jest
jest
A) 5 B) 7 C) 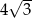 D)
D) 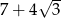
Liczba  jest ujemna, a liczba
jest ujemna, a liczba 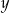 jest dodatnia. Wartość ujemną przyjmuje wyrażenie
jest dodatnia. Wartość ujemną przyjmuje wyrażenie
A) 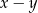 B)
B) 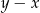 C)
C) 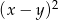 D)
D) 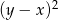
Liczba pierwiastków wielomianu 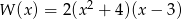 jest równa
jest równa
A) 4 B) 3 C) 2 D) 1
Funkcje 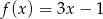 i
i 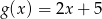 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 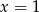 B)
B) 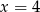 C)
C) 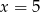 D)
D) 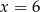
Wykres funkcji 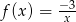 znajduje się w ćwiartkach
znajduje się w ćwiartkach
A) II i IV B) II i III C) I i III D) I i II
Zbiorem wartości funkcji 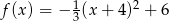 jest
jest
A) 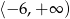 B)
B) 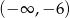 C)
C) 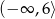 D)
D) 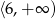
W ciągu arytmetycznym o różnicy 4 siódmy wyraz wynosi 33. Pierwszy wyraz tego ciągu jest równy
A) 5 B) 9 C) 29 D) 132
Liczby 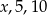 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 2,5 B) 5 C) 10 D) 0
Wartość wyrażenia 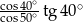 wynosi
wynosi
A) 1 B) 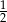 C)
C) 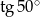 D)
D) 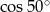
Jeżeli wysokość trójkąta równobocznego wynosi 2, to długość jego boku jest równa
A) 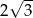 B)
B) 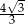 C)
C) 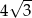 D) 6
D) 6
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 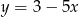 jest równy
jest równy
A) 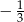 B) 3 C) -5 D)
B) 3 C) -5 D) 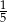
Podstawą ostrosłupa czworokątnego jest kwadrat o boku 4. Krawędź boczna o długości 9 jest prostopadła do podstawy. Objętość tego ostrosłupa wynosi:
A) 144 B) 48 C) 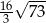 D)
D) 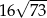
Objętość walca o promieniu podstawy  i wysokości 2 razy większej od promienia jest równa
i wysokości 2 razy większej od promienia jest równa
A) 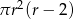 B)
B) 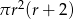 C)
C) 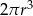 D)
D) 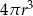
Pan Jakub ma 4 marynarki, 7 par różnych spodni i 10 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 280 B) 21 C) 28 D) 70
Wyniki konkursu matematycznego podano w punktach: 94, 92, 90, 90, 86, 86, 86, 72. Medianą tego zestawu wyników jest
A) 86 B) 88 C) 92 D) 94
Na loterii jest 10 losów, z których 4 są wygrywające. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A)  B)
B)  C)
C)  D)
D) 
Zadania otwarte
Uzasadnij, że jeżeli prostokąt 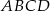 nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.
nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.

W kwadracie 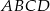 dane są wierzchołek
dane są wierzchołek 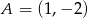 i środek symetrii
i środek symetrii 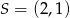 . Oblicz pole kwadratu
. Oblicz pole kwadratu 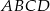 .
.
Rzucamy czerwoną i zieloną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na wyrzuceniu takiej samej liczby oczek na obu kostkach.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 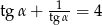 , oblicz
, oblicz 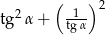 .
.
Wyznacz wszystkie liczby całkowite spełniające nierówność 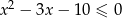 .
.
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 18 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 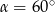 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.
Wyznacz wzór funkcji 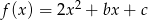 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 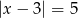 .
.
Szkoła zamówiła seans filmowy dla uczniów klas trzecich. Koszt seansu wyniósł 1650 zł. Ponieważ do kina nie przyszło 15 uczniów, pozostali musieli dopłacić po 1 zł za bilet. Jaka była planowana, a jaka rzeczywista cena biletów?
Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny, w którym środkowy wyraz jest równy 8. Wyznacz długości boków trójkąta, oblicz jego pole oraz promień okręgu opisanego na tym trójkącie.

