/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 25 kwietnia 2009 Czas pracy: 120 minut

Zadanie 1
(5 pkt)

Dany jest wykres funkcji 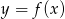y = f(x) określonej dla x ∈ ⟨− 7,7⟩ .

PIC

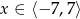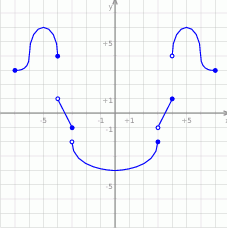
Odczytaj z wykresu:

  • rozwiązania równania f(x − 1) = 1 ;
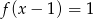  • miejsca zerowe funkcji y = f(x) + 2 ;
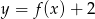  • maksymalne przedziały monotoniczności funkcji f (x) .

Zadanie 2
(4 pkt)

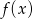Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna ma długość 18 cm i tworzy z bokiem odpowiadającym wysokości walca kąt o mierze 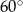∘ 60 . Oblicz objętość walca.

Zadanie 3
(5 pkt)

Eksperymentalna kolonia bakterii liczyła przed 16 dniami 65536 bakterii, a obecnie liczy 390625 bakterii. O ile procent przeciętnie wzrasta liczba bakterii w tej kolonii w ciągu jednego dnia? (Zakładamy stały przyrost procentowy). Wynik podaj z dokładnością do 1%.

Zadanie 4
(6 pkt)

Pewna maszyna wykonuje śruby o średnicy 14 mm. Dokonano kontroli jakości wykonywanych śrub i jej wyniki zebrano w tabeli.

Średnica w mm13,813,91414,114,2
Liczba śrub 8 17 48 13 14

Opierając się na podanych danych.

  • Oblicz średnią średnicę śruby.
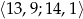  • Oblicz prawdopodobieństwo wyprodukowania śruby o średnicy z przedziału ⟨13 ,9;14,1⟩ .
  • Oblicz odchylenie standardowe średnicy śruby. Wynik podaj z dokładnością do 0,01.

Zadanie 5
(5 pkt)

Na rysunku prosta 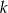k przechodzi przez punkt P (−6 ,−3 ) .

PIC

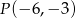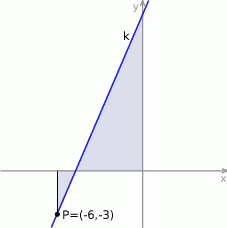
Wiedząc, że stosunek pól zacieniowanych trójkątów prostokątnych jest równy 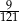9121-

  • oblicz pola tych trójkątów;
  • wyznacz równanie prostej k .

Zadanie 6
(5 pkt)
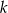  • Suma kwadratów trzech kolejnych ujemnych liczb całkowitych parzystych jest równa 116. Wyznacz te liczby.
  • Wyznacz takie trzy kolejne liczby całkowite parzyste, których suma kwadratów jest najmniejsza z możliwych.

Zadanie 7
(4 pkt)

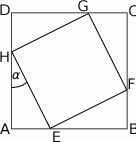
W kwadrat 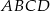ABCD o boku długości 17 wpisano kwadrat 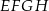EF GH , jak pokazano na rysunku. Wiedząc, że przekątna kwadratu 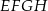EF GH ma długość 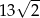-- 13√ 2 oblicz tangens kąta α zaznaczonego na rysunku.

PIC

Zadanie 8
(3 pkt)

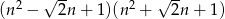Uzasadnij, że jeżeli n jest liczbą całkowitą to liczba 2 √ -- 2 √ -- (n − 2n + 1 )(n + 2n + 1) też jest liczbą całkowitą.

Zadanie 9
(5 pkt)

Fabryka odzieży w pierwszym roku produkcji wyprodukowała 2000 kurtek i 1000 par spodni. W każdym kolejnym roku produkcję par spodni zwiększano o 400 sztuk, a produkcję kurtek zmniejszano o 20%. Po ilu latach produkcji łączna liczba (od początku działalności fabryki) wyprodukowanych par spodni przekroczy łączną liczbę wyprodukowanych kurtek?

Zadanie 10
(5 pkt)

Spawacz ma wykonać z blachy konstrukcję, która powstaje przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego trójkątnego. Wymiary elementów są podane na rysunku.

PIC

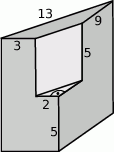
  • Oblicz objętość tej konstrukcji.
  • Oblicz łączne pole powierzchni wszystkich 7 ścian otrzymanej bryły. Wynik podaj z zaokrągleniem do 2 1 cm .

Zadanie 11
(3 pkt)

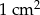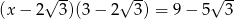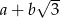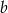Rozwiąż równanie √ -- √ -- √ -- (x − 2 3 )(3− 2 3) = 9 − 5 3 . Wynik przedstaw w postaci √ -- a + b 3 , gdzie a i b są liczbami całkowitymi.

Arkusz Wersja PDF
Rozwiązania