/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom podstawowy grupa I 23 maja 2018 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 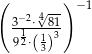 jest równa
jest równa
A) 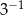 B)
B) 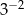 C)
C) 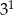 D)
D) 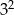
Suma liczby  i jej kwadratu jest najmniejsza dla liczby
i jej kwadratu jest najmniejsza dla liczby  równej
równej
A) 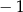 B)
B) 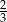 C)
C) 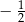 D)
D) 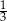
Iloczyn liczby 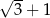 i odwrotności liczby
i odwrotności liczby 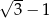 jest równy
jest równy
A) 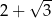 B)
B) 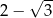 C)
C) 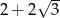 D)
D) 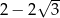
Cenę książki obniżano dwukrotnie, najpierw o 10%, a po miesiącu jeszcze o 5%. W wyniku obu obniżek cena książki zmniejszyła się o
A) 14% B) 14,5% C) 15% D) 15,5%
Wartość liczbowa wyrażenia 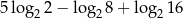 jest równa
jest równa
A) 1 B) 2 C) 6 D) 8
Liczba 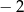 jest miejscem zerowym funkcji liniowej
jest miejscem zerowym funkcji liniowej 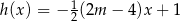 . Wynika stąd, że
. Wynika stąd, że
A) 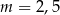 B)
B) 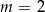 C)
C) 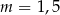 D)
D) 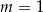
Na rysunku przedstawiona jest prosta, przechodząca przez punkty 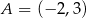 i
i 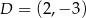 , oraz zaznaczony jest kąt
, oraz zaznaczony jest kąt  nachylenia tej prostej do osi
nachylenia tej prostej do osi 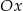 .
.
Zatem tangens kąta  jest równy
jest równy
A)  B)
B) 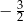 C)
C)  D)
D) 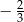
Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest
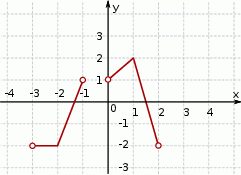
A) 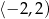 B)
B) 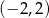 C)
C) 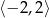 D)
D) 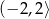
Obwód trójkąta równobocznego jest równy 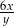 , gdzie
, gdzie 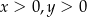 . Pole powierzchni tego trójkąta jest równe
. Pole powierzchni tego trójkąta jest równe
A) 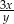 B)
B) 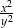 C)
C) 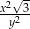 D)
D) 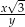
Dziedziną funkcji 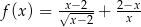 jest
jest
A) 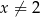 B)
B) 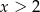 C)
C) 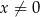 D)
D) 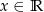
Miara kąta  pod jakim przecinają się styczne do okręgu o środku
pod jakim przecinają się styczne do okręgu o środku 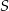 wynosi
wynosi
A) 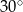 B)
B) 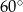 C)
C) 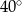 D)
D) 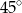
Jeżeli 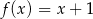 i
i 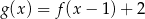 , to funkcja
, to funkcja 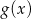 jest równa
jest równa
A) 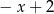 B)
B) 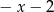 C)
C) 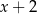 D)
D) 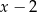
Wśród podanych poniżej nierówności wskaż tę, której zbiorem rozwiązań jest przedział 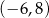 .
.
A) 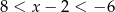 B)
B) 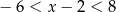 C)
C) 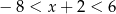 D)
D) 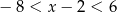
Punkt 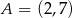 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 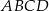 , a punkt
, a punkt 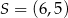 jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A) 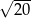 B)
B) 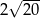 C)
C) 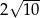 D)
D) 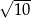
Wiadomo, że 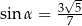 i
i 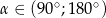 . Wynika stąd, że
. Wynika stąd, że
A) 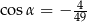 B)
B) 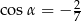 C)
C) 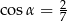 D)
D) 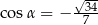
Na rysunku proste 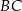 i
i 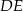 są równoległe oraz
są równoległe oraz 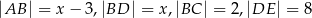 . Wobec tego
. Wobec tego  jest równe
jest równe
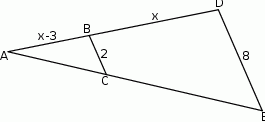
A) 3 B) 3,5 C) 4 D) 4,5
Dany jest trzywyrazowy ciąg geometryczny o wyrazach dodatnich: 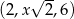 . Wówczas
. Wówczas
A) 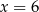 B)
B) 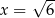 C)
C) 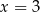 D)
D) 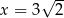
Dany jest ciąg liczbowy 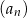 , w którym
, w którym 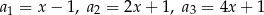 . Dla jakiej wartości liczbowej
. Dla jakiej wartości liczbowej  dany ciąg jest ciągiem arytmetycznym?
dany ciąg jest ciągiem arytmetycznym?
A) 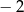 B) 2 C) 3 D) 4
B) 2 C) 3 D) 4
Jeżeli 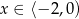 , to wartość wyrażenia
, to wartość wyrażenia 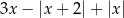 jest równa
jest równa
A) 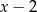 B)
B) 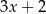 C)
C) 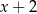 D)
D) 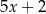
Setny wyraz ciągu 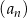 jest równy 2018. Wzór ogólny na
jest równy 2018. Wzór ogólny na  -ty wyraz ciągu
-ty wyraz ciągu 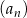 może mieć postać
może mieć postać
A) 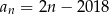 B)
B) 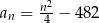 C)
C) 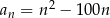 D)
D) 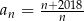
Do wykresu funkcji 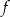 danej wzorem
danej wzorem 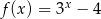 , należy punkt o współrzędnych
, należy punkt o współrzędnych
A) 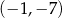 B)
B) 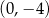 C)
C) 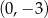 D)
D) 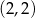
Piąty wyraz rosnącego ciągu geometrycznego jest równy 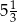 , a siódmy
, a siódmy 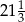 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 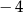 B) 2 C)
B) 2 C) 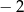 D) 4
D) 4
Na okręgu o środku w punkcie 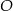 leżą punkty
leżą punkty 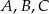 (zobacz rysunek).
(zobacz rysunek).
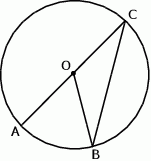
Odcinek 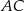 jest średnicą okręgu. Kąt
jest średnicą okręgu. Kąt 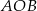 ma miarę
ma miarę 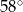 . Kąt
. Kąt 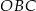 ma miarę równą
ma miarę równą
A) 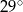 B)
B) 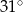 C)
C) 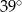 D)
D) 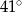
Dany jest trapez równoramienny (patrz rysunek). Wtedy 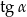 jest równy
jest równy
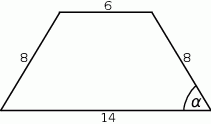
A) 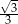 B)
B) 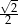 C)
C) 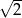 D)
D) 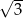
Funkcja kwadratowa określona jest wzorem 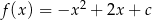 . Jeżeli
. Jeżeli 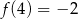 , to
, to
A) 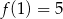 B)
B) 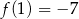 C)
C) 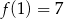 D)
D) 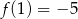
Zadania otwarte
Wyznacz zbiór nieujemnych rozwiązań nierówności 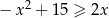 .
.
Wykaż, że trójkąt 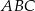 o wierzchołkach
o wierzchołkach 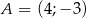 ,
, 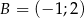 ,
, 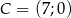 jest prostokątny.
jest prostokątny.
Oblicz obwód trójkąta prostokątnego o polu powierzchni równym 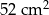 , wiedząc, że długości jego przyprostokątnych różnią się o 5 cm.
, wiedząc, że długości jego przyprostokątnych różnią się o 5 cm.
Wyrazami ciągu arytmetycznego 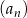 są kolejne liczby naturalne, które przy dzieleniu przez 7 dają resztę 3. Ponadto
są kolejne liczby naturalne, które przy dzieleniu przez 7 dają resztę 3. Ponadto 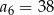 . Oblicz
. Oblicz 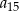 .
.
Ojciec i syn mają łącznie 52 lata. Sześć lat temu ojciec był trzykrotnie starszy od syna. Ile lat ma ojciec, a ile syn?
Wykaż, że jeżeli środkowa trójkąta jest dwa razy krótsza od boku, do którego jest poprowadzona, to trójkąt ten jest prostokątny.
Na prostej o równaniu 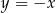 wyznacz współrzędne punktu
wyznacz współrzędne punktu 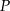 leżącego najbliżej punktu
leżącego najbliżej punktu 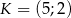 .
.
W wyniku zwiększenia każdego boku danego prostokąta o 2 cm jego pole wzrosło o 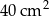 . O ile zwiększy się pole danego prostokąta, jeśli jego boki zwiększymy o 3 cm?
. O ile zwiększy się pole danego prostokąta, jeśli jego boki zwiększymy o 3 cm?
Na okręgu o promieniu 2 opisano trójkąt prostokątny o jednej z przyprostokątnych długości 12. Oblicz obwód tego trójkąta.

