/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 4 marca 2017 Czas pracy: 170 minut
Zadania zamknięte
Suma sześciu kolejnych liczb całkowitych jest równa 189. Najmniejszą z tych liczb jest
A) 32 B) 31 C) 30 D) 29
W pewnym zakładzie pracy w wyniku dwóch podwyżek zwiększono pensje pracowników o 26%. W ramach pierwszej z tych podwyżek płace zwiększono o 20%. O ile procent zwiększono płace w ramach drugiej podwyżki?
A) o 12% B) o 6% C) o 5% D) o 10%
Liczba 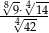 jest równa
jest równa
A) 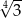 B)
B) 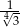 C) 1 D) 3
C) 1 D) 3
Równość 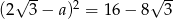 jest prawdziwa dla
jest prawdziwa dla
A) 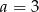 B)
B) 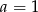 C)
C) 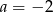 D)
D) 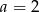
Ciąg 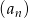 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 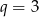 , w którym
, w którym 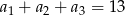 . Suma
. Suma 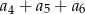 jest równa
jest równa
A) 39 B) 351 C) 117 D) 507
Wartość wyrażenia 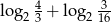 jest równa
jest równa
A) 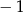 B)
B) 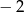 C)
C) 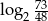 D)
D) 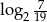
Punkty 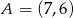 i
i 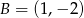 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 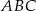 . Promień koła opisanego na tym trójkącie jest równy
. Promień koła opisanego na tym trójkącie jest równy
A) 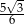 B)
B) 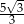 C)
C) 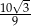 D)
D) 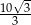
Która z liczb jest rozwiązaniem równania 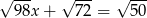 ?
?
A) 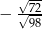 B)
B) 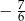 C)
C) 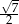 D)
D) 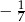
Dany jest zbiór 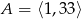 . Liczb pierwszych, które należą do tego zbioru jest
. Liczb pierwszych, które należą do tego zbioru jest
A) 9 B) 10 C) 11 D) 12
Dana jest funkcja kwadratowa 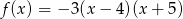 . Wskaż maksymalny przedział, w którym funkcja
. Wskaż maksymalny przedział, w którym funkcja 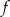 jest malejąca.
jest malejąca.
A) 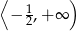 B)
B) 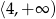 C)
C) 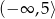 D)
D) 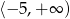
Równanie 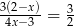 nie ma takiego samego rozwiązania, jak równanie
nie ma takiego samego rozwiązania, jak równanie
A) 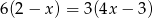
B) 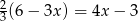
C) 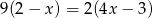
D) 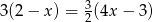
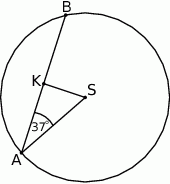
W okręgu o środku w punkcie 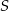 poprowadzono cięciwę
poprowadzono cięciwę 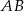 , która utworzyła z promieniem
, która utworzyła z promieniem 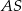 kąt o mierze
kąt o mierze 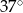 (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu
(zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu 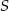 od cięciwy
od cięciwy 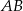 jest liczbą z przedziału
jest liczbą z przedziału
A) 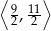 B)
B) 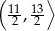 C)
C) 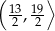 D)
D) 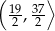
W nieskończonym ciągu arytmetycznym wyraz o numerze 2017 jest o 348 mniejszy od wyrazu o numerze 1930. Różnica tego ciągu jest równa
A) 87 B) 4 C) 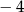 D)
D) 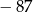
Dany jest trapez prostokątny 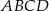 , w którym
, w którym 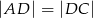 oraz
oraz 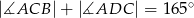 (zobacz rysunek).
(zobacz rysunek).
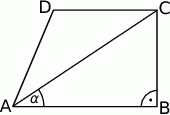
Stąd wynika, że
A) 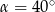 B)
B) 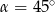 C)
C) 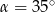 D)
D) 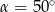
Ile jest liczb naturalnych pięciocyfrowych, których iloczyn cyfr jest równy 70?
A) 60 B) 36 C) 12 D) 125
Szklane naczynie w kształcie stożka o promieniu podstawy 6 cm i wysokości 9 cm napełniono wodą do  wysokości (zobacz rysunek).
wysokości (zobacz rysunek).
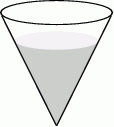
Objętość wody w naczyniu jest równa
A) 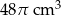 B)
B) 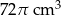 C)
C) 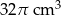 D)
D) 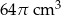
Jeżeli  jest kątem ostrym pod jakim przecinają się proste
jest kątem ostrym pod jakim przecinają się proste 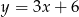 i
i 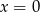 , to
, to
A) 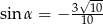 B)
B) 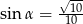 C)
C) 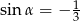 D)
D) 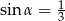
Układ równań 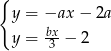 nie ma rozwiązania dla
nie ma rozwiązania dla
A) 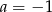 i
i 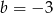 B)
B) 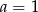 i
i 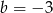 C)
C) 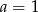 i
i 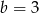 D)
D) 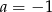 i
i 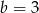
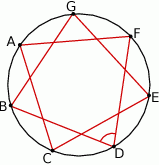
Punkty 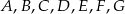 okręgu są wierzchołkami siedmiokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
okręgu są wierzchołkami siedmiokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 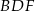 jest równa
jest równa
A) 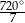 B)
B) 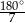 C)
C) 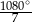 D)
D) 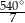
Mediana zestawu liczb: 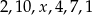 zmniejsza się o 1 po usunięciu liczby
zmniejsza się o 1 po usunięciu liczby  . Wtedy
. Wtedy
A) 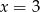 B)
B) 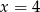 C)
C) 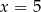 D)
D) 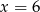
W układzie współrzędnych dane są punkty 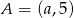 oraz
oraz 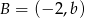 . Środkiem odcinka
. Środkiem odcinka 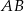 jest punkt
jest punkt 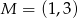 . Wynika stąd, że
. Wynika stąd, że
A) 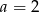 i
i 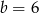 B)
B) 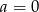 i
i 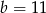 C)
C) 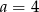 i
i 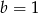 D)
D) 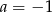 i
i 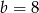
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 4, a przekątna ściany bocznej ma długość 5 (zobacz rysunek). Kąt, jaki tworzą przekątna ściany bocznej i przekątna podstawy wychodzące z jednego wierzchołka, ma miarę  .
.
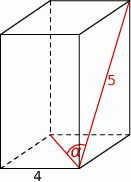
Wtedy wartość 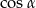 jest równa
jest równa
A)  B)
B) 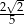 C)
C) 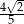 D)
D) 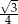
Na podstawie 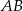 i ramieniu
i ramieniu 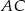 trójkąta równoramiennego
trójkąta równoramiennego 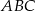 dane są punkty
dane są punkty 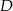 i
i 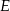 takie, że
takie, że 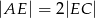 i
i 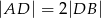 . Punkty
. Punkty 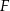 i
i 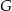 leżą na ramieniu
leżą na ramieniu 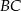 tak, że odcinki
tak, że odcinki 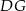 i
i 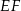 są prostopadłe do prostej
są prostopadłe do prostej 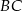 (zobacz rysunek).
(zobacz rysunek).
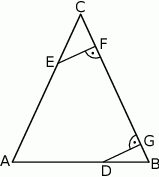
Pole trójkąta 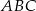 jest równe 18. Zatem suma pól trójkątów
jest równe 18. Zatem suma pól trójkątów 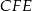 i
i 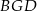 jest równa
jest równa
A) 9 B) 6 C) 3 D) 2
Średnia arytmetyczna dziesięciu kolejnych liczb naturalnych jest równa 15,5. Mediana tych liczb jest równa
A) 15,5 B) 31 C) 16 D) 16,5
Na rysunku przedstawione są dwie proste równoległe 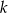 i
i 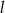 o równaniach
o równaniach 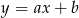 oraz
oraz 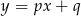 . Początek układu współrzędnych leży między tymi prostymi.
. Początek układu współrzędnych leży między tymi prostymi.
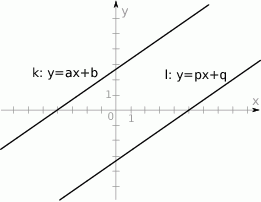
Zatem
A) 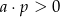 i
i 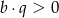
B) 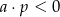 i
i 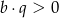
C) 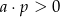 i
i 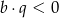
D) 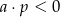 i
i 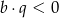
Zadania otwarte
Dane są proste o równaniach 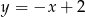 oraz
oraz 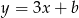 , które przecinają się w punkcie leżącym na osi
, które przecinają się w punkcie leżącym na osi 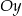 układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi
układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi 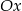 .
.
Wykaż, że jeżeli dwusieczne dwóch sąsiednich kątów wewnętrznych czworokąta wypukłego są prostopadłe, to czworokąt ten jest trapezem.
Wyznacz wszystkie liczby całkowite spełniające nierówność 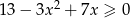 .
.
Wykaż, że jeżeli liczby rzeczywiste 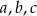 spełniają warunek
spełniają warunek 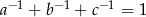 , to
, to
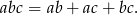
Suma miar dwóch sąsiednich kątów trapezu jest równa 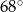 , a różnica miar dwóch pozostałych kątów jest równa
, a różnica miar dwóch pozostałych kątów jest równa 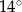 . Oblicz miary kątów tego trapezu.
. Oblicz miary kątów tego trapezu.
Funkcja kwadratowa 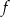 ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu
ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu 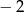 , a do jej wykresu należy punkt
, a do jej wykresu należy punkt 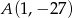 . Napisz wzór funkcji
. Napisz wzór funkcji 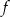 w postaci ogólnej.
w postaci ogólnej.
Losujemy jedną liczbę całkowitą z przedziału 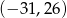 i jedną liczbę całkowitą z przedziału
i jedną liczbę całkowitą z przedziału 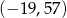 . Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni. Wynik podaj w postaci ułamka nieskracalnego.
. Oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb, których iloczyn jest dodatni. Wynik podaj w postaci ułamka nieskracalnego.
Dwie partie konserw rybnych, liczące po 1440 konserwy każda, zapakowano w kartony. Każdą z partii zapakowano w ten sposób, że w każdym kartonie znalazła się ta sama liczba konserw, przy czym w przypadku drugiej partii liczbę kartonów zmniejszono o 2 i w kartonach umieszczono o 10 konserw więcej, niż w przypadku kartonów pierwszej partii. Do ilu łącznie kartonów zapakowano te dwie partie konserw?
Dany jest stożek o objętości 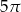 , w którym stosunek wysokości do promienia podstawy jest równy 5:9. Oblicz pole powierzchni bocznej tego stożka.
, w którym stosunek wysokości do promienia podstawy jest równy 5:9. Oblicz pole powierzchni bocznej tego stożka.

