/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 20 marca 2021 Czas pracy: 170 minut
Zadania zamknięte
Liczba 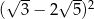 jest równa
jest równa
A) 11 B) 7 C) 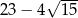 D)
D) 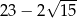
Do przedziału 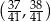 należy liczba
należy liczba
A) 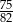 B)
B) 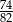 C)
C) 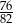 D)
D) 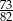
Liczba 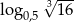 jest równa
jest równa
A) 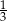 B)
B) 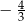 C)
C) 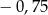 D) 1,5
D) 1,5
Zbiorem rozwiązań nierówności 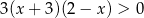 jest zbiór zaznaczony na osi liczbowej:
jest zbiór zaznaczony na osi liczbowej:

Wyrażenie 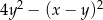 jest równe wyrażeniu:
jest równe wyrażeniu:
A) 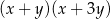 B)
B) 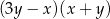 C)
C) 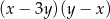 D)
D) 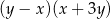
W wyniku dwóch obniżek cenę komputera obniżono o 40%. Druga z tych obniżek była obniżką o 25%. O ile procent obniżono cenę komputera przy pierwszej obniżce?
A) o 15% B) o 65% C) o 20% D) o 30%
Informacja do zadań 7 – 9
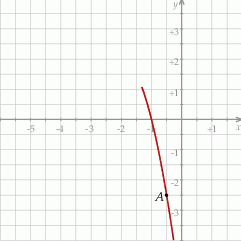
Funkcja kwadratowa 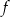 jest określona wzorem
jest określona wzorem 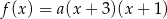 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 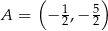 .
.
Współczynnik  we wzorze funkcji
we wzorze funkcji 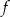 jest równy
jest równy
A) 1 B) 2 C) 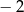 D)
D) 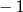
Najmniejsza wartość funkcji 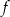 w przedziale
w przedziale 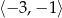 jest równa
jest równa
A) 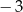 B) 0 C)
B) 0 C) 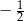 D)
D) 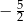
Osią symetrii paraboli będącej wykresem funkcji 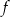 jest prosta o równaniu
jest prosta o równaniu
A) 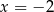 B)
B) 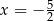 C)
C) 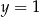 D)
D) 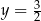
Funkcje liniowe 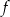 i
i 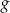 określone wzorami
określone wzorami 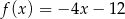 i
i 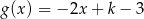 mają wspólne miejsce zerowe. Stąd wynika, że
mają wspólne miejsce zerowe. Stąd wynika, że
A) 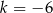 B)
B) 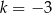 C)
C) 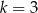 D)
D) 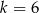
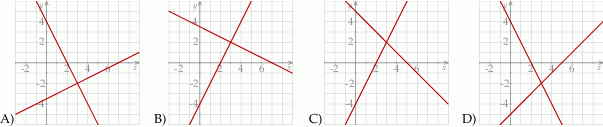
Ilustracja graficzna układu równań 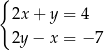 jest przedstawiona na rysunku:
jest przedstawiona na rysunku:
Funkcja 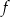 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący iloczynem dwóch różnych liczb pierwszych. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący iloczynem dwóch różnych liczb pierwszych. Spośród liczb: 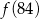 ,
, 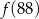 ,
, 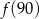 ,
, 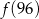 największa to
największa to
A) 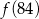 B)
B) 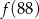 C)
C) 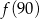 D)
D) 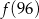
Proste o równaniach 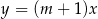 oraz
oraz 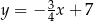 są równoległe. Wtedy
są równoległe. Wtedy
A) 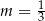 B)
B) 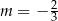 C)
C) 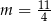 D)
D) 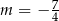
Przez punkt 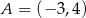 poprowadzono prostą
poprowadzono prostą 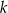 , która przecina proste
, która przecina proste 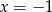 i
i 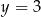 w takich punktach
w takich punktach 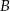 i
i 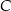 , że
, że 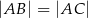 . Długość odcinka
. Długość odcinka 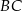 jest równa
jest równa
A) 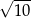 B)
B) 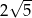 C)
C) 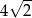 D)
D) 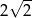
Siedem liczb tworzy ciąg geometryczny. Iloczyn tych liczb jest równy 2187. Czwarty wyraz tego ciągu jest równy
A) 243 B) 9 C) 3 D) 27
Punkty 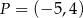 i
i 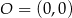 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem nachylenia tej prostej do osi
jest kątem nachylenia tej prostej do osi 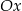 (zobacz rysunek).
(zobacz rysunek).
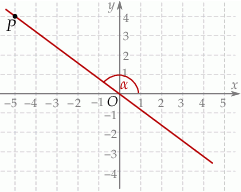
Wtedy tangens kąta  jest równy
jest równy
A)  B)
B)  C)
C) 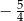 D)
D) 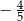
Cięciwy 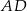 i
i 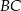 okręgu o środku
okręgu o środku 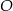 przecinają się w punkcie
przecinają się w punkcie 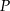 tak, że
tak, że 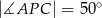 (zobacz rysunek).
(zobacz rysunek).
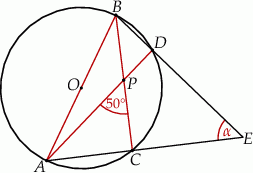
Jeżeli punkt 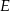 jest punktem wspólnym prostych
jest punktem wspólnym prostych 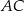 i
i 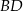 , to miara kąta
, to miara kąta 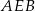 jest równa
jest równa
A) 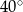 B)
B) 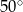 C)
C) 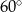 D)
D) 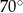
Wartość wyrażenia 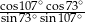 wynosi
wynosi
A) 1 B) 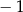 C)
C) 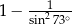 D)
D) 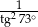
W ciągu arytmetycznym 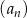 , określonym dla
, określonym dla 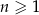 , spełniony jest warunek
, spełniony jest warunek 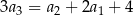 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 4 B) 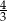 C) 2 D)
C) 2 D) 
W trójkącie prostokątnym o przyprostokątnych długości 7 i 24 połączono wierzchołek 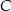 kąta prostego ze środkiem
kąta prostego ze środkiem 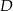 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 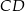 jest równa
jest równa
A) 25 B) 12 C) 15 D) 12,5
Ile jest wszystkich trzycyfrowych liczb naturalnych utworzonych z cyfr: 1, 3, 5, 7, 9, w których cyfry się nie powtarzają?
A) 60 B) 125 C) 120 D) 95
W prostokątnym układzie współrzędnych na płaszczyźnie parę prostych prostopadłych opisują równania
A) 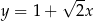 i
i 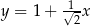 B)
B) 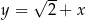 i
i 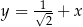
C) 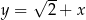 i
i 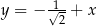 D)
D) 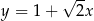 i
i 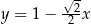
Prawdopodobieństwo zdarzenia 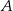 jest 5 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 5 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 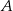 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 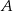 jest równe
jest równe
A) 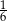 B)
B) 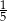 C)
C) 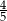 D)
D) 
Ciąg 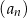 jest określony wzorem
jest określony wzorem 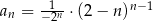 . Zatem
. Zatem
A) 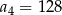 B)
B) 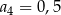 C)
C) 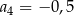 D)
D) 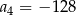
Dwa stożki o takich samych podstawach połączono podstawami z podstawami walca w taki sposób jak na rysunku. Wysokość mniejszego z tych stożków jest taka sama jak wysokość walca i stanowi  wysokości większego ze stożków. Objętość całej bryły jest równa
wysokości większego ze stożków. Objętość całej bryły jest równa 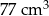 .
.
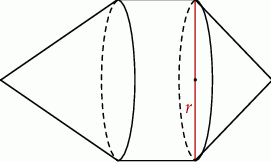
Objętość walca jest równa
A) 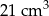 B)
B) 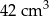 C)
C) 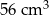 D)
D) 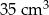
Średnia arytmetyczna danych przedstawionych na diagramie częstości jest równa
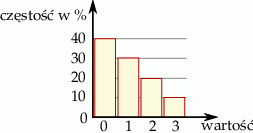
A) 1 B) 1,2 C) 1,5 D) 1,8
Pole powierzchni całkowitej sześcianu jest równe 9. Suma długości wszystkich krawędzi tego sześcianu jest równa
A) 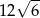 B)
B) 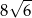 C)
C) 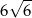 D)
D) 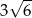
Prawdopodobieństwo, że w czterokrotnym rzucie symetryczną monetą otrzymamy trzy reszki i jednego orła, jest równe
A) 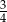 B) 0,375 C) 0,25 D)
B) 0,375 C) 0,25 D) 
Zadania otwarte
Liczba  jest dodatnim pierwiastkiem równania
jest dodatnim pierwiastkiem równania 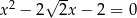 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
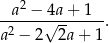
Rozwiąż nierówność: 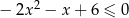 .
.
Wykaż, że dla dowolnego kąta  ,
,
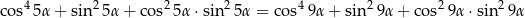
Trójkąt 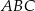 jest równoboczny. Punkt
jest równoboczny. Punkt 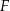 leży na wysokości
leży na wysokości 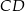 tego trójkąta oraz
tego trójkąta oraz 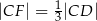 . Punkt
. Punkt 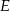 leży na boku
leży na boku 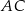 i odcinek
i odcinek 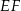 jest prostopadły do
jest prostopadły do 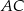 (zobacz rysunek).
(zobacz rysunek).
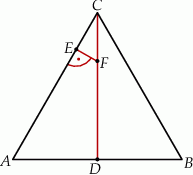
Wykaż, że 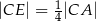 .
.
W prostopadłościanie pola trzech ścian o wspólnym wierzchołku są równe 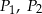 i
i  . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
W układzie współrzędnych na płaszczyźnie punkty 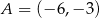 i
i 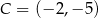 są przeciwległymi wierzchołkami deltoidu
są przeciwległymi wierzchołkami deltoidu 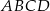 , w którym
, w którym 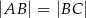 . Wyznacz równanie prostej
. Wyznacz równanie prostej 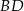 .
.
Wyrazy niezerowego ciągu geometrycznego 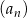 , określonego dla
, określonego dla 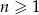 spełniają warunki:
spełniają warunki: 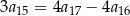 oraz
oraz 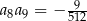 . Oblicz iloczyn pierwszych sześciu wyrazów tego ciągu.
. Oblicz iloczyn pierwszych sześciu wyrazów tego ciągu.

