/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 25 kwietnia 2009 Czas pracy: 180 minut
Przekątne trapezu o podstawach długości 1 i 2 są prostopadłe. Oblicz sumę kwadratów długości przekątnych trapezu.
Rozwiąż układ równań 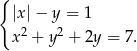
Rozważmy cięciwy 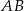 paraboli
paraboli 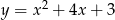 przechodzące przez punkt
przechodzące przez punkt 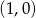 , przy czym przez cięciwę
, przy czym przez cięciwę 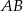 rozumiemy prostą przecinającą tę parabolę w dwóch punktach
rozumiemy prostą przecinającą tę parabolę w dwóch punktach 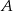 i
i 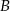 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 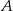 i
i 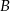 , dla których suma współrzędnych środka odcinka
, dla których suma współrzędnych środka odcinka 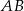 cięciwy
cięciwy 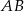 jest równa
jest równa 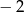 .
.
Dla jakich liczb 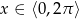 liczby
liczby 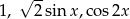 są trzema kolejnymi wyrazami ciągu geometrycznego?
są trzema kolejnymi wyrazami ciągu geometrycznego?
Ze zbioru 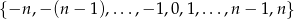 , gdzie
, gdzie 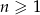 losujemy dwie liczby (mogą się powtarzać). Oblicz jakie jest prawdopodobieństwo, że suma wartości bezwzględnych wylosowanych liczb jest nie większa niż
losujemy dwie liczby (mogą się powtarzać). Oblicz jakie jest prawdopodobieństwo, że suma wartości bezwzględnych wylosowanych liczb jest nie większa niż  .
.
Wyznacz wszystkie liczby całkowite 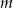 , dla których równanie
, dla których równanie
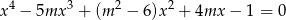
nie ma rozwiązań wymiernych.
Uporządkuj rosnąco liczby 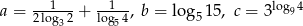 .
.
W czworokącie 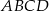 o obwodzie 24 dane są
o obwodzie 24 dane są 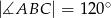 oraz
oraz 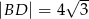 . Wiedząc, że środek przekątnej
. Wiedząc, że środek przekątnej 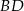 jest środkiem symetrii tego czworokąta oblicz jego pole.
jest środkiem symetrii tego czworokąta oblicz jego pole.
Ciąg 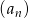 jest ciągiem arytmetycznym o różnicy 2, a ciąg
jest ciągiem arytmetycznym o różnicy 2, a ciąg 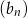 zdefiniowany jest wzorem
zdefiniowany jest wzorem 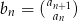 , dla
, dla 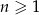 . Wyznacz wartość
. Wyznacz wartość  , dla której
, dla której 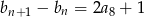 .
.
Wyznacz największą wartość funkcji 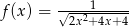 .
.
Pole powierzchni całkowitej stożka jest trzy razy większe od pola jego podstawy. Oblicz stosunek objętości stożka do objętości wpisanej w niego kuli.

