/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 10 marca 2018 Czas pracy: 180 minut
Zadania zamknięte
Liczba 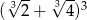 jest równa
jest równa
A) 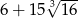 B)
B) 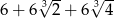 C)
C) 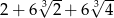 D)
D) 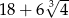
Równanie 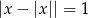 ? ma
? ma
A) nieskończenie wiele rozwiązań.
B) jedno rozwiązanie.
C) dwa rozwiązania.
D) zero rozwiązań.
Jeżeli  jest takim kątem rozwartym, że
jest takim kątem rozwartym, że 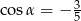 , to liczba
, to liczba 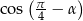 jest równa
jest równa
A) 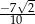 B)
B) 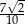 C)
C) 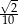 D)
D) 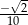
Dane są punkt 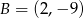 i wektor
i wektor ![→ v = [− 10 ,6]](https://img.zadania.info/zes/0058373/HzesT14x.gif) . Punkt
. Punkt 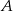 , taki, że
, taki, że 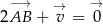 , ma współrzędne
, ma współrzędne
A) 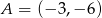 B)
B) 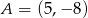 C)
C) 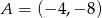 D)
D) 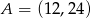
Funkcja 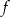 jest określona wzorem
jest określona wzorem 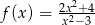 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 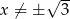 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 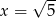 jest równa
jest równa
A) 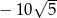 B)
B) 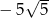 C)
C) 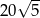 D)
D) 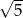
Zadania otwarte
Oblicz granicę funkcji 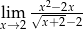 .
.
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 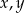 prawdziwa jest nierówność
prawdziwa jest nierówność
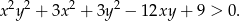
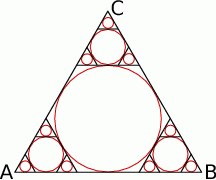
W trójkąt równoboczny 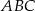 o boku długości 1 wpisano koło. Prowadzimy proste równoległe do boków trójkąta
o boku długości 1 wpisano koło. Prowadzimy proste równoległe do boków trójkąta 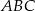 i styczne do koła wpisanego. Proste te odcinają od trójkąta
i styczne do koła wpisanego. Proste te odcinają od trójkąta  trzy trójkąty równoboczne. W każdy z nich wpisujemy koło i postępujemy analogicznie jak z kołem wpisanym w trójkąt
trzy trójkąty równoboczne. W każdy z nich wpisujemy koło i postępujemy analogicznie jak z kołem wpisanym w trójkąt  . Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich otrzymanych w ten sposób kół.
. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich otrzymanych w ten sposób kół.
Wykaż, że jeżeli odcinki łączące środki przeciwległych boków czworokąta są prostopadłe, to przekątne tego czworokąta mają równe długości.
Między liczby 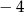 i 36 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
i 36 wstaw dwie liczby tak, aby trzy pierwsze tworzyły ciąg arytmetyczny, a trzy ostatnie ciąg geometryczny.
Karol do szyfrowania swoich danych postanowił używać pięciocyfrowych liczb naturalnych  , które mają co najmniej jedną z dwóch cech: w zapisie dziesiętnym liczby
, które mają co najmniej jedną z dwóch cech: w zapisie dziesiętnym liczby  występuje przynajmniej jedna z cyfr: 3, 4, 5, 6, 7, 8, 9, lub liczba
występuje przynajmniej jedna z cyfr: 3, 4, 5, 6, 7, 8, 9, lub liczba  nie jest podzielna przez 3. Ile jest takich liczb pięciocyfrowych?
nie jest podzielna przez 3. Ile jest takich liczb pięciocyfrowych?
W urnie jest 7 kul czarnych i 3 białe. Losujemy z tej urny pięć razy po jednej kuli i po każdym losowaniu wkładamy wylosowaną kulę z powrotem do urny oraz dokładamy do urny dwie kule w kolorze wylosowanej kuli. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwa razy wylosujemy kulę białą.
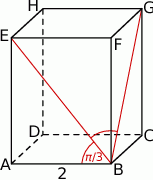
Przekątna 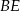 ściany bocznej prostopadłościanu
ściany bocznej prostopadłościanu 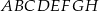 tworzy z krawędzią podstawy
tworzy z krawędzią podstawy 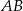 kąt o mierze
kąt o mierze 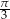 . Przekątne
. Przekątne 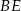 i
i 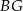 ścian bocznych tworzą kąt, którego cosinus jest równy
ścian bocznych tworzą kąt, którego cosinus jest równy 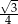 , a krawędź
, a krawędź 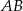 podstawy ma długość 2. Oblicz promień okręgu opisanego na trójkącie
podstawy ma długość 2. Oblicz promień okręgu opisanego na trójkącie 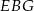 .
.
Wyznacz wszystkie wartości parametru 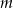 , dla których równanie
, dla których równanie
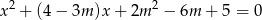
ma dwa różne rozwiązania takie, że każde należy do przedziału 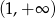 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 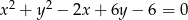 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 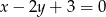 .
.
Rozpatrujemy wszystkie stożki, których pole powierzchni całkowitej jest równe 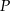 . Oblicz wysokość i promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
. Oblicz wysokość i promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.

