/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy+ 19 marca 2011 Czas pracy: 170 minut
Zadania zamknięte
Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.
![]()
A) 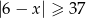 B)
B) 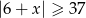 C)
C) 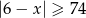 D)
D) 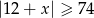
Zmieszano 15 g 20% roztworu z 25 g 12% roztworu. Stężenie procentowe otrzymanego roztworu jest równe
A) 15% B) 14% C) 16% D) 18%
Różnica 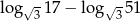 jest równa
jest równa
A) -2 B) 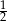 C) 2 D)
C) 2 D) 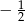
Połowa liczby 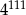 to
to
A) 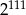 B)
B) 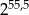 C)
C) 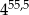 D)
D) 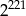
Wyrażenie 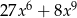 można zapisać w postaci
można zapisać w postaci
A) 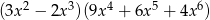
B) 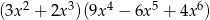
C) 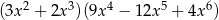
D) 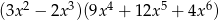
Rozwiązaniem równania 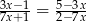 jest
jest
A) 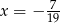 B)
B) 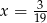 C)
C) 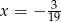 D)
D) 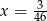
Zbiorem rozwiązań nierówności 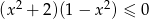 jest
jest
A) 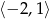 B)
B) 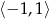 C)
C) 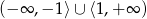 D)
D) 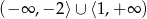
Proste o równaniach 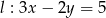 i
i 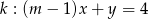 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 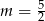 B)
B) 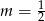 C)
C) 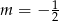 D)
D) 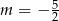
Wierzchołek paraboli o równaniu 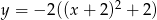 ma współrzędne
ma współrzędne
A) 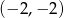 B)
B) 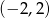 C)
C) 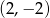 D)
D) 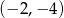
Na rysunku poniżej przedstawiony jest wykres funkcji liniowej 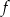 .
.
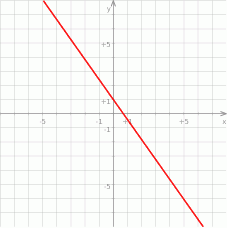
Funkcja to może być określona wzorem
A) 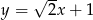 B)
B) 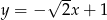 C)
C) 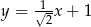 D)
D) 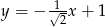
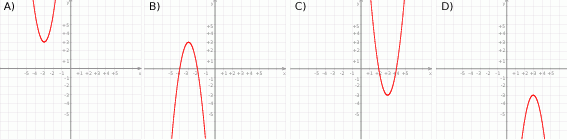
Funkcja 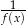 jest określona na całym zbiorze liczb rzeczywistych i nie przyjmuje wartości dodatnich. Na którym rysunku przedstawiono wykres funkcji
jest określona na całym zbiorze liczb rzeczywistych i nie przyjmuje wartości dodatnich. Na którym rysunku przedstawiono wykres funkcji 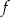 ?
?
Wyrazami ciągu 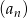 danego wzorem
danego wzorem 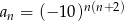
A) są zawsze liczby mniejsze od 1
B) są zawsze liczby dodatnie
C) są zawsze liczby ujemne
D) są zarówno liczby dodatnie, jak i ujemne
Liczba  jest liczbą naturalną większą od 2 i
jest liczbą naturalną większą od 2 i 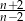 jest liczbą naturalną. Z tego wynika, że liczbą naturalną jest również liczba
jest liczbą naturalną. Z tego wynika, że liczbą naturalną jest również liczba
A) 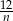 B)
B) 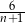 C)
C) 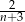 D)
D) 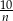
Wybieramy liczbę  ze zbioru
ze zbioru 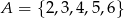 oraz liczbę
oraz liczbę 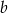 ze zbioru
ze zbioru 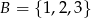 . Ile jest takich par
. Ile jest takich par 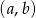 , że iloczyn
, że iloczyn 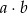 jest liczbą parzystą?
jest liczbą parzystą?
A) 11 B) 21 C) 5 D) 9
Boki 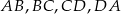 czworokąta
czworokąta 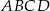 są odpowiednio zawarte w prostych o równaniach
są odpowiednio zawarte w prostych o równaniach 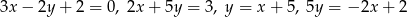 . Wtedy czworokąt
. Wtedy czworokąt 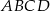
A) jest równoległobokiem, który nie jest rombem
B) jest rombem
C) jest trapezem, który nie jest równoległobokiem
D) nie jest trapezem
Kąt  jest ostry oraz
jest ostry oraz 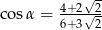 . Wtedy
. Wtedy 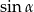 jest równy
jest równy
A) 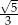 B)
B) 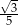 C)
C) 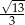 D)
D) 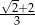
Punkty 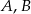 i
i 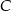 leżą na okręgu o środku
leżą na okręgu o środku 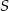 (zobacz rysunek).
(zobacz rysunek).
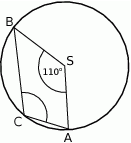
Miara zaznaczonego kąta wpisanego 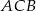 jest równa
jest równa
A) 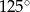 B)
B) 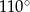 C)
C) 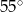 D)
D) 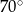
Przekątne trapezu 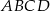 przecinają się w punkcie
przecinają się w punkcie 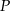 w ten sposób, że
w ten sposób, że 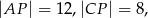
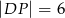 . Długość odcinka
. Długość odcinka 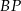 jest równa
jest równa
A) 18 B) 16 C) 9 D) 8
Suma długości wszystkich krawędzi i wszystkich przekątnych ścian sześcianu jest równa 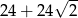 . Jaka jest objętość tego sześcianu?
. Jaka jest objętość tego sześcianu?
A) 8 B) 27 C) 64 D) 96
Prawdopodobieństwo zdarzenia 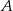 jest o 0,1 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do
jest o 0,1 większe od połowy prawdopodobieństwa zdarzenia przeciwnego do 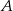 . Zatem
. Zatem 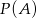 jest równe
jest równe
A) 0,6 B) 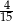 C) 0,4 D)
C) 0,4 D) 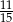
Zadania otwarte
Rozwiąż nierówność 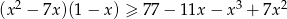 .
.
Rozwiąż równanie 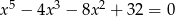 .
.
Kąta  jest ostry oraz
jest ostry oraz 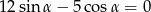 . Oblicz
. Oblicz 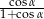 .
.
Rzucamy trzy razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w trzecim rzucie otrzymamy dwa razy więcej oczek niż w pierwszym rzucie.
Oblicz promień okręgu opisanego na trójkącie o wierzchołkach 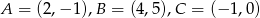 .
.
Wykaż, że liczba 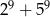 jest podzielna przez 133.
jest podzielna przez 133.
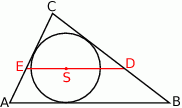
Przez środek 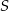 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 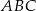 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 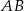 , która przecina boki
, która przecina boki 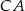 i
i 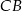 odpowiednio w punktach
odpowiednio w punktach 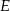 i
i 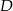 .
.
Wykaż, że 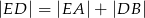 .
.
W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 6, a pole ściany bocznej jest równe 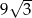 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Ciąg 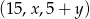 jest arytmetyczny, natomiast ciąg
jest arytmetyczny, natomiast ciąg 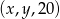 jest geometryczny. Oblicz
jest geometryczny. Oblicz  oraz
oraz 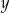 i podaj ten ciąg geometryczny.
i podaj ten ciąg geometryczny.
Boki trójkąta 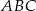 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 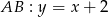 ,
, 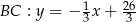 i
i 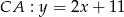 . Wyznacz współrzędne środka okręgu opisanego na trójkącie
. Wyznacz współrzędne środka okręgu opisanego na trójkącie 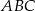 .
.

