/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom podstawowy grupa I 31 maja 2011 Czas pracy: 170 minut
Zadania zamknięte
Dla którego z podanych zbiorów liczb naturalnych wyrażenie 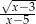 ma sens liczbowy?
ma sens liczbowy?
A) 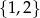 B)
B) 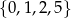 C)
C) 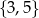 D)
D) 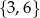
Średnia arytmetyczna liczb: 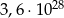 i
i 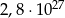 jest równa:
jest równa:
A) 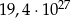 B)
B) 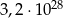 C)
C) 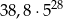 D)
D) 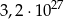
Współczynnikiem liczbowym jednomianu 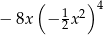 jest liczba
jest liczba
A) 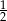 B) 4 C)
B) 4 C) 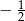 D)
D) 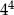
Wykres funkcji kwadratowej 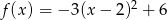 przecina oś
przecina oś 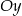 w punkcie o współrzędnych:
w punkcie o współrzędnych:
A) 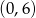 B)
B) 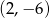 C)
C) 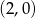 D)
D) 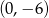
Ile punktów wspólnych z osią 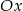 ma wykres funkcji kwadratowej
ma wykres funkcji kwadratowej 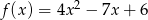 ?
?
A) 0 B) 1 C) 2 D) 3
Ile pierwiastków ma wielomian 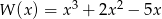 ?
?
A) 0 B) 1 C) 2 D) 3
Dane są wielomiany: 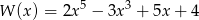 i
i 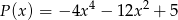 . Stopień wielomianu
. Stopień wielomianu 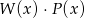 jest równy:
jest równy:
A) 20 B) -8 C) 9 D) 5
Funkcja
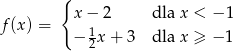
dla argumentu 2 przyjmuje wartość:
A) 0 B) 2 C) 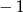 D) 4
D) 4
W trapezie prostokątnym kąt ostry ma miarę 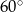 . Wysokość tego trapezu jest równa 3 cm. O ile centymetrów dłuższa jest jedna podstawa od drugiej?
. Wysokość tego trapezu jest równa 3 cm. O ile centymetrów dłuższa jest jedna podstawa od drugiej?
A) 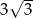 B) 6 C) 3 D)
B) 6 C) 3 D) 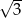
Miejscem zerowym funkcji liniowej 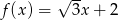 jest liczba:
jest liczba:
A) 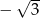 B) -2 C)
B) -2 C) 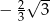 D)
D) 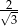
Z naczynia napełnionego wodą, odlano 4,2 l wody. Woda, która pozostała w naczyniu zajmuje 65% jego pojemności. Zatem pojemność tego naczynia wynosi:
A) 12 l B) 11 l C) 13 l D) 11,5 l
Dla pewnego kąta ostrego zachodzi 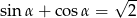 . Wtedy
. Wtedy 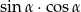 jest równy:
jest równy:
A) 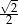 B)
B) 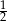 C)
C) 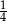 D) 1
D) 1
Stosunek pól kół wpisanego i opisanego na kwadracie o boku długości  jest równy:
jest równy:
A) 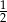 B)
B) 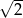 C)
C) 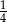 D)
D) 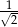
Wartością wyrażenia 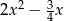 dla
dla 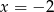 jest liczba:
jest liczba:
A) 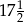 B)
B) 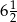 C)
C) 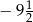 D)
D) 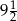
Do wykresu funkcji 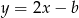 należy punkt
należy punkt 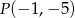 . Współczynnik
. Współczynnik 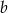 jest równy:
jest równy:
A) -3 B) 3 C) -7 D) -5
Dany jest ciąg arytmetyczny, w którym 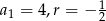 . Wtedy
. Wtedy
A) 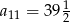 B)
B) 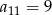 C)
C) 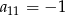 D)
D) 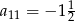
Liczba 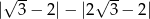 jest równa
jest równa
A) 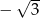 B)
B) 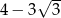 C)
C) 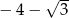 D)
D) 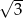
Zbiorem rozwiązań nierówności 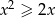 jest:
jest:
A) 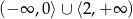 B)
B) 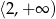 C)
C) 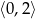 D)
D) 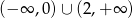
Współczynnikiem kierunkowym prostej o równaniu 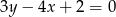 jest liczba:
jest liczba:
A) 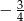 B)
B) 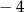 C)
C) 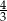 D)
D) 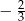
Liczba 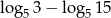 wynosi:
wynosi:
A) 1 B) 0 C) 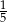 D) -1
D) -1
Promień okręgu opisanego na prostokącie o bokach: 6 cm i 8 cm jest równy:
A) 7 cm B) 6,5 cm C) 5 cm D) 10 cm
Jeżeli liczby 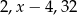 tworzą rosnący ciąg geometryczny, to
tworzą rosnący ciąg geometryczny, to
A) 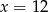 B)
B) 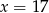 C)
C) 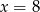 D)
D) 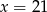
Do wykresu funkcji 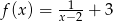 , należy punkt o współrzędnych:
, należy punkt o współrzędnych:
A) 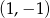 B)
B) 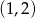 C)
C) 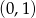 D)
D) 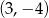
Osią symetrii paraboli o równaniu 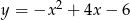 jest prosta:
jest prosta:
A) 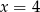 B)
B) 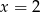 C)
C) 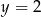 D)
D) 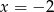
Rozwiązaniem równania 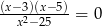 jest liczba:
jest liczba:
A) 3 B) -5 C) 5 D) 0
Zadania otwarte
Podaj wymiary prostokąta, którego boki różnią się o 6 cm, a przekątna ma długość 30 cm.
Oblicz  z równania
z równania 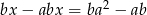 i przedstaw wynik w najprostszej postaci.
i przedstaw wynik w najprostszej postaci.
Rozwiąż nierówność: 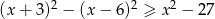 .
.
Do okręgu należy punkt 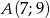 , oraz jest on styczny do osi
, oraz jest on styczny do osi 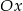 w punkcie
w punkcie 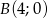 . Podaj równanie tego okręgu.
. Podaj równanie tego okręgu.
Wykaż, że 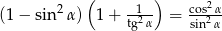 .
.
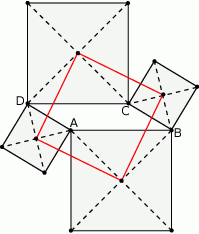
Wykazać, że odcinki łączące kolejne środki kwadratów zbudowanych na bokach równoległoboku tworzą także kwadrat.
Na okręgu o promieniu 9 opisano trójkąt równoramienny o kącie równym 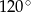 . Oblicz długości boków trójkąta.
. Oblicz długości boków trójkąta.
Basen można napełnić dwoma kranami w ciągu 6 godzin. Pierwszy kran napełnia basen w czasie o 5 godzin krótszym niż drugi. W ciągu ilu godzin, każdy kran oddzielnie napełni basen.
Jedno z rozwiązań równania 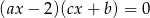 jest równe 6. Ciąg
jest równe 6. Ciąg 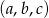 jest ciągiem arytmetycznym, w którym pierwszy wyraz jest o 8 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.
jest ciągiem arytmetycznym, w którym pierwszy wyraz jest o 8 większy od trzeciego. Znajdź drugie rozwiązanie tego równania.

