/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 16 kwietnia 2011 Czas pracy: 180 minut
Wykaż, że jeżeli 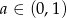 i
i 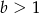 to prawdziwa jest nierówność
to prawdziwa jest nierówność
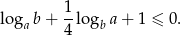
Ciąg 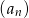 , gdzie
, gdzie 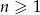 dany jest wzorem rekurencyjnym
dany jest wzorem rekurencyjnym
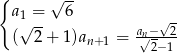
- Oblicz sumę 21 początkowych wyrazów tego ciągu.
- Wyznacz wszystkie liczby naturalne
 , dla których spełniona jest nierówność
, dla których spełniona jest nierówność 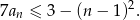
Dwa okręgi przecinają się w punktach 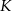 i
i 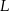 . Przez punkty
. Przez punkty 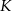 i
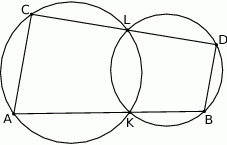
i 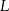 poprowadzono proste, które przecinają dane okręgi w punktach
poprowadzono proste, które przecinają dane okręgi w punktach 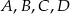 tak, jak pokazano to na poniższym rysunku. Wykaż, że
tak, jak pokazano to na poniższym rysunku. Wykaż, że 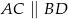 .
.
Wyznacz resztę z dzielenia wielomianu 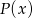 przez trójmian
przez trójmian 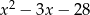 jeśli
jeśli 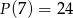 i
i 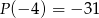 .
.
Prosta o równaniu 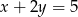 zawiera przekątną
zawiera przekątną 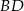 rombu
rombu 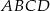 , którego bok ma długość 5. Wyznacz współrzędne wierzchołków rombu jeżeli
, którego bok ma długość 5. Wyznacz współrzędne wierzchołków rombu jeżeli 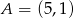 .
.
Dla jakich wartości parametru 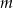 równanie
równanie 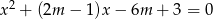 ma dwa różne pierwiastki
ma dwa różne pierwiastki 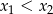 spełniające nierówność
spełniające nierówność 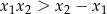 .
.
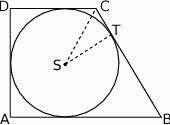
W trapez prostokątny 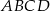 wpisano okrąg, przy czym punkt
wpisano okrąg, przy czym punkt 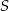 jest środkiem tego okręgu, a punkt
jest środkiem tego okręgu, a punkt 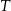 jest punktem styczności okręgu wpisanego z dłuższym ramieniem
jest punktem styczności okręgu wpisanego z dłuższym ramieniem 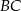 . Oblicz pole tego trapezu, jeśli
. Oblicz pole tego trapezu, jeśli 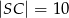 i
i 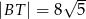 .
.
Dla jakich liczb naturalnych  , liczba
, liczba 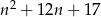 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
Podstawą ostrosłupa 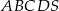 jest czworokąt wypukły
jest czworokąt wypukły 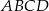 , w którym
, w którym 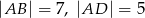 oraz
oraz 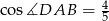 . Każda z krawędzi bocznych ostrosłupa ma długość
. Każda z krawędzi bocznych ostrosłupa ma długość 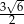 . Oblicz wysokość ostrosłupa.
. Oblicz wysokość ostrosłupa.
Ile jest liczb dziewięciocyfrowych, w których suma każdych trzech kolejnych cyfr jest równa 10?

