/Szkoła średnia/Zadania maturalne

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 2 maja 2009 Czas pracy: 120 minut

Zadanie 1
(3 pkt)

Wysokość trójkąta prostokątnego poprowadzona na przeciwprostokątną dzieli ją na odcinki długości 1 cm i 49 cm. Oblicz pole tego trójkąta.

Zadanie 2
(5 pkt)

Dane są punkty 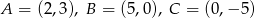A = (2,3), B = (5,0), C = (0,− 5) .

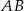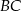  • Uzasadnij, że proste AB i BC są prostopadłe.
  • Wyznacz współrzędne takiego punktu 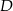D , dla którego czworokąt 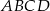ABCD jest prostokątem.
  • Oblicz pole prostokąta ABCD .

Zadanie 3
(5 pkt)

Dany jest wielomian 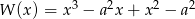W (x) = x3 − a2x + x2 − a2 , gdzie |a| ⁄= 1 .

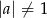  • Oblicz sumę pierwiastków tego wielomianu.
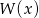  • Wyznacz wartość parametru a , dla której suma kwadratów pierwiastków wielomianu W (x) jest możliwie najmniejsza.

Zadanie 4
(4 pkt)

Sprawdź, czy liczby 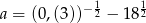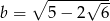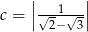− 1 1 a = (0,(3)) 2 − 182 , ∘ -----√--- b = 5 − 2 6 , | | |---1---| c = |√ 2−√ 3| są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.

Zadanie 5
(5 pkt)

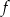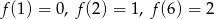Funkcja f przyporządkowuje każdej liczbie naturalnej dodatniej liczbę jej dzielników będących liczbami pierwszymi. Np. f (1) = 0, f(2) = 1, f(6) = 2 .

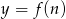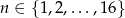  • Naszkicuj wykres funkcji y = f (n) dla n ∈ {1,2,...,16} .
  • Podaj przykład liczby n , dla której f(n ) = 4 .
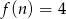  • Uzasadnij, że równanie 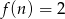f(n ) = 2 ma nieskończenie wiele rozwiązań.

Zadanie 6
(4 pkt)

Ze zbioru liczb naturalnych pięciocyfrowych wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 15.

Zadanie 7
(3 pkt)

Janek kupił dwie książki, które po roku sprzedał ze stratą 10%. Wiedząc, że pierwszą z nich sprzedał ze stratą 25%, a drugą z zyskiem 12,5% oblicz, o ile procent pierwsza książka była droższa od drugiej (w chwili zakupu).

Zadanie 8
(3 pkt)

Do naczynia w kształcie walca wypełnionego wodą do wysokości 7 cm włożono metalową kulkę o promieniu 3 cm. Poziom wody podniósł się o 1 cm i zrównał się z górną podstawą walca. Oblicz objętość naczynia. Przyjmując 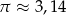π ≈ 3,14 , wynik podaj z dokładnością do 3 1 cm .

Zadanie 9
(4 pkt)

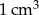W ciągu geometrycznym 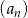(a ) n dane są iloraz 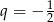q = − 1 2 oraz suma

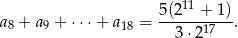
5 (211 + 1) a8 + a9 + ⋅ ⋅⋅+ a18 =------17-- . 3⋅2

Oblicz 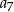a 7 .

Zadanie 10
(4 pkt)

Rozwiąż nierówność 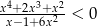x4+-2x3+x-2< 0 x− 1+6x2 .

Zadanie 11
(3 pkt)

Uzasadnij, że jeżeli dwie dwusieczne trójkąta przecinają się pod kątem 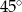45∘ to trójkąt jest prostokątny.

Zadanie 12
(4 pkt)

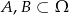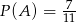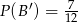Niech A ,B ⊂ Ω będą zdarzeniami losowymi, takimi że P(A ) = -7 11 i P (B′) = -7 12 . Uzasadnij, że P (A ∩ B ) > 0 .

Zadanie 13
(3 pkt)

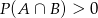Czy kwadratową płytą o boku długości 2,2 m można całkowicie zakryć otwór w ziemi, który ma kształt stożka o wysokości 2 m i kącie rozwarcia 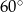∘ 6 0 ?

PIC

Odpowiedź uzasadnij.

Arkusz Wersja PDF
Rozwiązania