/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony 2 czerwca 2022 Czas pracy: 180 minut
Zadania zamknięte
Wiadomo, że 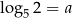 oraz
oraz 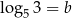 . Wtedy liczba
. Wtedy liczba 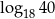 jest równa
jest równa
A) 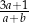 B)
B) 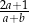 C)
C) 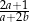 D)
D) 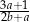
Granica 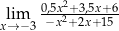 jest równa
jest równa
A) 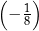 B)
B) 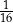 C)
C) 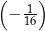 D)
D) 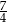
Sumą wektorów ![→ [ 2 ] a = 2 + 2m ,3n + 1](https://img.zadania.info/zes/0059955/HzesT12x.png) oraz
oraz ![→ b = [n + 1,m + 2]](https://img.zadania.info/zes/0059955/HzesT13x.png) jest wektor
jest wektor ![→ c = [0,0]](https://img.zadania.info/zes/0059955/HzesT14x.png) . Wynika stąd, że
. Wynika stąd, że
A) 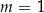 i
i 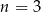 B)
B) 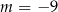 i
i 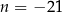 C)
C) 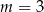 i
i 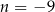 D)
D) 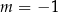 i
i 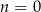
Pole trójkąta ostrokątnego o bokach 5 i 6 jest równe 9. Długość trzeciego boku tego trójkąta jest równa
A) 5 B) 6 C) 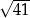 D)
D) 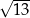
Zadania otwarte
Wśród 390 pracowników pewnej firmy jest 150 kobiet i 240 mężczyzn. Wśród nich w wieku przedemerytalnym jest 21 kobiet i 43 mężczyzn. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany pracownik tej firmy jest w wieku przedemerytalnym – pod warunkiem że jest mężczyzną.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 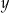 takich, że
takich, że 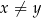 , spełniona jest nierówność
, spełniona jest nierówność
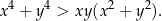
Oblicz, ile jest wszystkich liczb naturalnych pięciocyfrowych, w których zapisie występują dokładnie dwie cyfry nieparzyste.
Rozwiąż nierówność
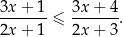
W trapezie 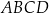 o podstawach
o podstawach 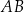 i
i 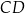 przez punkt
przez punkt 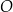 przecięcia się przekątnych poprowadzono dwie proste równoległe do boków
przecięcia się przekątnych poprowadzono dwie proste równoległe do boków 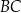 i
i 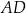 . Prosta równoległa do boku
. Prosta równoległa do boku 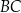 przecina bok
przecina bok 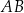 w punkcie
w punkcie 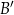 , a prosta równoległa do boku
, a prosta równoległa do boku 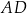 przecina bok
przecina bok 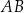 w punkcie
w punkcie 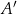 . Wykaż, że
. Wykaż, że 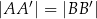 .
.
Dany jest nieskończony ciąg geometryczny 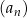 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 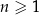 , którego iloraz
, którego iloraz 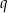 jest równy pierwszemu wyrazowi i spełnia warunek
jest równy pierwszemu wyrazowi i spełnia warunek  . Stosunek sumy
. Stosunek sumy 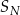 wszystkich wyrazów tego ciągu o numerach nieparzystych do sumy
wszystkich wyrazów tego ciągu o numerach nieparzystych do sumy 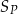 wszystkich wyrazów tego ciągu o numerach parzystych jest równy różnicy tych sum, tj.
wszystkich wyrazów tego ciągu o numerach parzystych jest równy różnicy tych sum, tj. 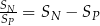 . Oblicz
. Oblicz 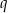 .
.
Rozwiąż równanie 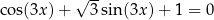 w przedziale
w przedziale 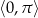 .
.
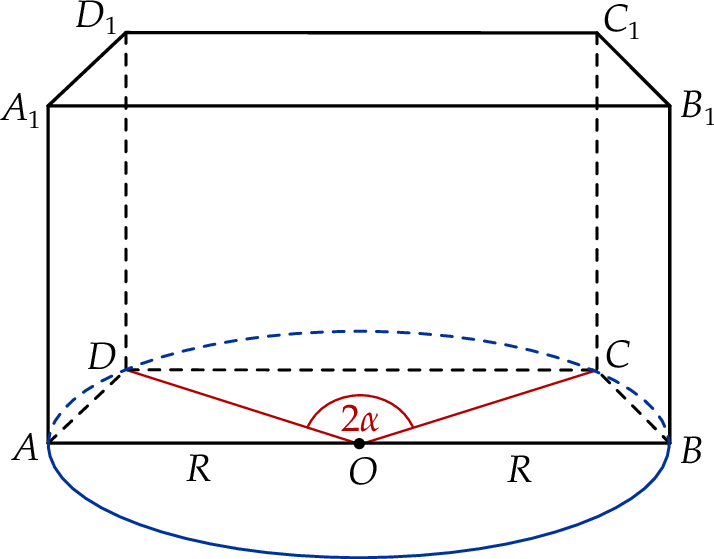
Podstawą graniastosłupa prostego 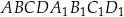 jest trapez równoramienny
jest trapez równoramienny 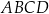 wpisany w okrąg o środku
wpisany w okrąg o środku 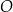 i promieniu
i promieniu 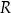 . Dłuższa podstawa
. Dłuższa podstawa 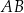 trapezu jest średnicą tego okręgu, a krótsza – cięciwą odpowiadającą kątowi środkowemu o mierze
trapezu jest średnicą tego okręgu, a krótsza – cięciwą odpowiadającą kątowi środkowemu o mierze 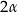 (zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze
(zobacz rysunek). Przekątna ściany bocznej zawierającej ramię trapezu jest nachylona do płaszczyzny podstawy pod kątem o mierze  . Wyznacz objętość tego graniastosłupa jako funkcję promienia
. Wyznacz objętość tego graniastosłupa jako funkcję promienia 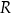 i miary kąta
i miary kąta  .
.
Wyznacz wszystkie wartości parametru 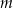 , dla których równanie
, dla których równanie
![(x − 4 )[x 2 + (m − 3)x + m 2 − m − 6] = 0](https://img.zadania.info/zes/0059955/HzesT64x.png)
ma trzy różne rozwiązania rzeczywiste 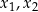 oraz
oraz 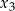 , spełniające warunek
, spełniające warunek
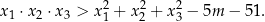
Dane są okrąg 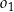 o równaniu
o równaniu 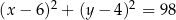 oraz okrąg
oraz okrąg 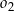 o promieniu
o promieniu 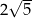 . Środki okręgów
. Środki okręgów 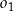 i
i 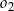 leżą po różnych stronach prostej
leżą po różnych stronach prostej 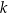 o równaniu
o równaniu 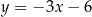 , a punkty wspólne obu okręgów leżą na prostej
, a punkty wspólne obu okręgów leżą na prostej 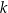 . Wyznacz równanie okręgu
. Wyznacz równanie okręgu 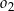 .
.
Rozpatrujemy wszystkie trójkąty równoramienne ostrokątne 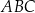 (
(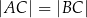 ), na których opisano okrąg o promieniu
), na których opisano okrąg o promieniu 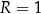 . Niech
. Niech  oznacza odległość środka okręgu od podstawy
oznacza odległość środka okręgu od podstawy 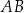 trójkąta.
trójkąta.
-
Wykaż, że pole
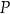 każdego z tych trójkątów, jako funkcja długości
każdego z tych trójkątów, jako funkcja długości  , wyraża się wzorem
, wyraża się wzorem 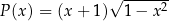 .
. -
Wyznacz dziedzinę funkcji
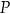 .
. -
Oblicz długość odcinka
 tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.
tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.

