/Szkoła średnia/Zadania maturalne
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom podstawowy 2 czerwca 2021 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 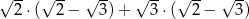 jest równa
jest równa
A) 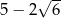 B) 5 C)
B) 5 C) 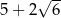 D)
D) 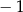
Liczba 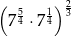 jest równa
jest równa
A) 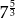 B)
B) 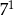 C)
C) 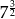 D)
D) 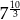
Niech 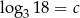 . Wtedy
. Wtedy 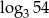 jest równy
jest równy
A) 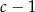 B)
B)  C)
C) 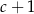 D)
D) 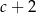
Cenę drukarki obniżono o 20%, a następnie nową cenę obniżono o 10%. W wyniku obu tych zmian cena drukarki zmniejszyła się w stosunku do ceny sprzed obu obniżek o
A) 18% B) 28% C) 30% D) 72%
Dla każdej liczby rzeczywistej  wyrażenie
wyrażenie 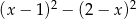 jest równe
jest równe
A) 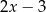 B)
B) 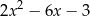 C)
C) 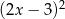 D) 9
D) 9
Wskaż rysunek, na którym przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających jednocześnie nierówności 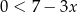 oraz
oraz 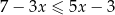 .
.
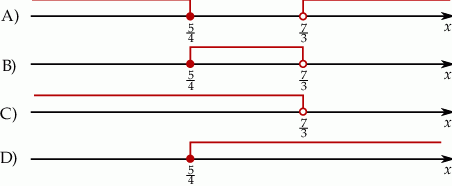
Rozwiązaniem równania 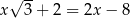 jest liczba
jest liczba
A) 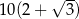 B)
B) 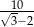 C)
C) 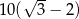 D)
D) 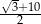
Równanie 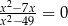 ma w zbiorze liczb rzeczywistych dokładnie
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Na rysunku przedstawiono wykres funkcji 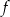 określonej w zbiorze
określonej w zbiorze 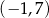 .
.
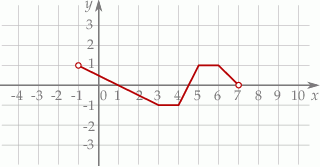
Wskaż zdanie prawdziwe.
A) Funkcja 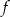 ma trzy miejsca zerowe.
ma trzy miejsca zerowe.
B) Zbiorem wartości funkcji 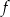 jest
jest 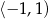 .
.
C) Funkcja 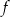 osiąga wartość największą równą 1.
osiąga wartość największą równą 1.
D) Funkcja 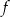 osiąga wartości ujemne dla argumentów ze zbioru
osiąga wartości ujemne dla argumentów ze zbioru 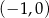 .
.
Wykresem funkcji kwadratowej 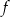 określonej wzorem
określonej wzorem 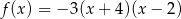 jest parabola o wierzchołku
jest parabola o wierzchołku 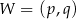 . Współrzędne wierzchołka
. Współrzędne wierzchołka 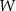 spełniają warunki
spełniają warunki
A) 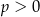 i
i 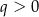 B)
B) 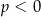 i
i 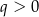 C)
C) 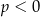 i
i 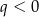 D)
D) 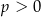 i
i 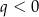
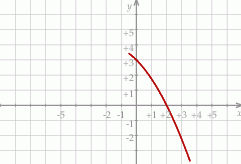
Informacja do zadań 11 i 12
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 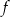 . Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji
. Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji 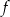 należy punkt
należy punkt 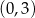 . Prosta o równaniu
. Prosta o równaniu 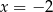 jest osią symetrii paraboli, będącej wykresem funkcji
jest osią symetrii paraboli, będącej wykresem funkcji 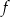 .
.
Drugim miejscem zerowym funkcji 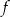 jest liczba
jest liczba
A) 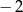 B)
B) 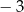 C)
C) 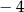 D)
D) 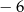
Wartość funkcji 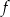 dla argumentu
dla argumentu 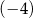 jest równa
jest równa
A) 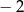 B) 0 C) 3 D) 4
B) 0 C) 3 D) 4
Dane są ciągi 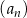 ,
, 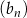 ,
, 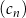 ,
, 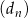 , określone dla każdej liczby naturalnej
, określone dla każdej liczby naturalnej 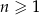 wzorami:
wzorami: 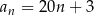 ,
, 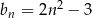 ,
, 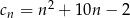 ,
, 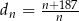 . Liczba 197 jest dziesiątym wyrazem ciągu
. Liczba 197 jest dziesiątym wyrazem ciągu
A) 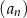 B)
B) 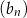 C)
C) 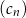 D)
D) 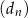
Ciąg geometryczny 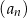 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 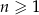 , jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek
, jest rosnący i wszystkie jego wyrazy są dodatnie. Ponadto spełniony jest warunek 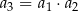 . Niech
. Niech 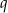 oznacza iloraz ciągu
oznacza iloraz ciągu 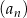 . Wtedy
. Wtedy
A) 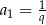 B)
B) 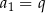 C)
C) 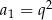 D)
D) 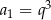
Kąt o mierze  jest ostry i
jest ostry i 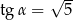 . Wtedy
. Wtedy
A) 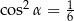 B)
B) 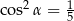 C)
C) 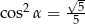 D)
D) 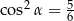
Na okręgu o środku w punkcie 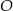 leżą punkty
leżą punkty 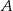 ,
, 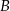 oraz
oraz 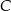 . Odcinek
. Odcinek 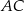 jest średnicą tego okręgu, a kąt środkowy
jest średnicą tego okręgu, a kąt środkowy 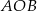 ma miarę
ma miarę 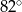 (zobacz rysunek).
(zobacz rysunek).
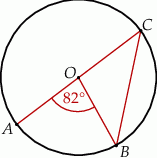
Miara kąta 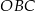 jest równa
jest równa
A) 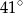 B)
B) 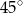 C)
C) 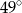 D)
D) 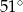
Dane są okrąg i prosta styczna do tego okręgu w punkcie 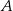 . Punkty
. Punkty 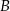 i
i 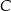 są położone na okręgu tak, że
są położone na okręgu tak, że 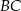 jest jego średnicą. Cięciwa
jest jego średnicą. Cięciwa 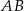 tworzy ze styczną kąt o mierze
tworzy ze styczną kąt o mierze 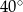 (zobacz rysunek).
(zobacz rysunek).
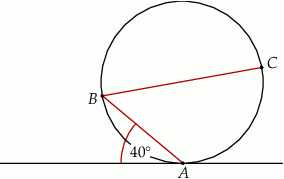
Miara kąta 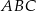 jest równa
jest równa
A) 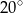 B)
B) 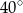 C)
C) 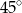 D)
D) 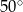
Dany jest trójkąt prostokątny 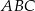 o bokach
o bokach 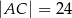 ,
, 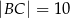 ,
, 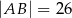 . Dwusieczne kątów tego trójkąta przecinają się w punkcie
. Dwusieczne kątów tego trójkąta przecinają się w punkcie 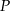 (zobacz rysunek).
(zobacz rysunek).
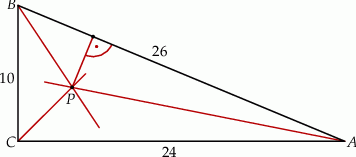
Odległość  punktu
punktu 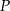 od przeciwprostokątnej
od przeciwprostokątnej 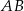 jest równa
jest równa
A) 2 B) 4 C)  D)
D) 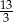
Jeden z boków równoległoboku ma długość równą 5. Przekątne tego równoległoboku mogą mieć długości
A) 4 i 6 B) 4 i 3 C) 10 i 10 D) 5 i 5
W pewnym trójkącie równoramiennym największy kąt ma miarę 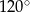 , a najdłuższy bok ma długość 12 (zobacz rysunek).
, a najdłuższy bok ma długość 12 (zobacz rysunek).
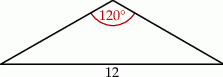
Najkrótsza wysokość tego trójkąta ma długość równą
A) 6 B) 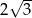 C)
C) 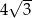 D)
D) 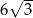
Prosta przechodząca przez punkty 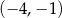 oraz
oraz 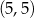 ma równanie
ma równanie
A) 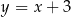 B)
B) 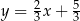 C)
C) 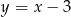 D)
D) 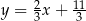
Proste o równaniach 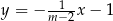 i
i 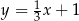 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 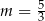 B)
B) 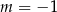 C)
C) 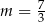 D)
D) 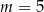
W prostokącie 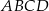 dane są wierzchołki
dane są wierzchołki 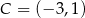 oraz
oraz 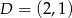 . Bok
. Bok 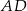 ma długość 6. Pole tego prostokąta jest równe
ma długość 6. Pole tego prostokąta jest równe
A) 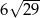 B)
B) 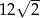 C) 24 D) 30
C) 24 D) 30
Obrazem prostej o równaniu 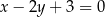 w symetrii osiowej względem osi
w symetrii osiowej względem osi 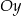 jest prosta o równaniu
jest prosta o równaniu
A) 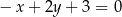 B)
B) 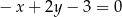 C)
C) 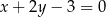 D)
D) 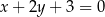
Graniastosłup prawidłowy ma 36 krawędzi. Długość każdej z tych krawędzi jest równa 4. Pole powierzchni bocznej tego graniastosłupa jest równe
A) 176 B) 192 C) 224 D) 288
Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy
A) 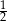 B)
B) 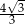 C) 1 D)
C) 1 D) 
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 25% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,75 B) 0,25 C) 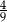 D)
D) 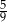
Średnia arytmetyczna czterech liczb dodatnich: 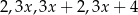 jest równa
jest równa 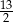 . Wynika stąd, że
. Wynika stąd, że
A) 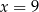 B)
B) 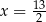 C)
C) 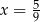 D)
D) 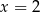
Zadania otwarte
Rozwiąż nierówność: 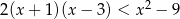 .
.
Wykaż, że dla wszystkich liczb rzeczywistych 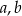 i
i  takich, że
takich, że 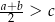 i
i 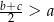 , prawdziwa jest nierówność
, prawdziwa jest nierówność
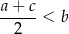
Dany jest ciąg arytmetyczny 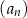 , określony dla wszystkich liczb naturalnych
, określony dla wszystkich liczb naturalnych 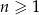 . Suma dwudziestu początkowych wyrazów tego ciągu jest równa
. Suma dwudziestu początkowych wyrazów tego ciągu jest równa 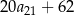 . Oblicz różnicę ciągu
. Oblicz różnicę ciągu 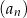 .
.
Dany jest trapez o podstawach długości  oraz
oraz 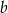 i wysokości
i wysokości 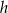 . Każdą z podstaw tego trapezu wydłużono o 25%, a wysokość skrócono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent skrócono wysokość
. Każdą z podstaw tego trapezu wydłużono o 25%, a wysokość skrócono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent skrócono wysokość 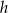 trapezu.
trapezu.
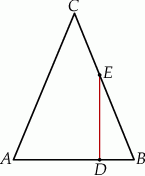
W trójkącie 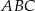 boki
boki 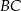 i
i 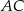 są równej długości. Prosta
są równej długości. Prosta 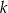 jest prostopadła do podstawy
jest prostopadła do podstawy 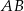 tego trójkąta i przecina boki
tego trójkąta i przecina boki 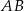 oraz
oraz 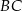 w punktach – odpowiednio –
w punktach – odpowiednio – 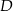 i
i 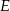 . Pole czworokąta
. Pole czworokąta 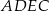 jest 17 razy większe od pola trójkąta
jest 17 razy większe od pola trójkąta 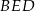 . Oblicz
. Oblicz 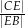 .
.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru 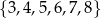 , a cyfra jedności należy do zbioru
, a cyfra jedności należy do zbioru 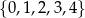 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.
Podstawa 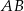 trójkąta równoramiennego
trójkąta równoramiennego 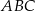 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 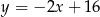 . Wierzchołki
. Wierzchołki 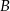 i
i 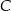 mają współrzędne
mają współrzędne 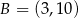 i
i 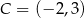 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 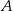 i pole trójkąta
i pole trójkąta 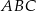 .
.

