/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 16 kwietnia 2016 Czas pracy: 180 minut
Zadania zamknięte
Ciąg 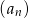 jest określony wzorem
jest określony wzorem 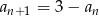 dla każdej liczby naturalnej
dla każdej liczby naturalnej 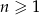 . Suma pięćdziesięciu początkowych wyrazów tego ciągu jest równa
. Suma pięćdziesięciu początkowych wyrazów tego ciągu jest równa
A) 150 B) 75 C) 50 D) 100
Dana jest funkcja  określona wzorem
określona wzorem 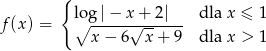
Równanie 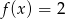 ma dokładnie
ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) trzy rozwiązania. D) cztery rozwiązania.
Suma
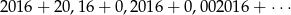
wszystkich wyrazów nieskończonego ciągu liczb rzeczywistych jest równa
A) 201600 B) 2240 C) 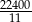 D)
D) 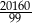
Na rysunku przedstawiono fragment wykresu pochodnej 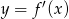 funkcji
funkcji 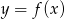 .
.
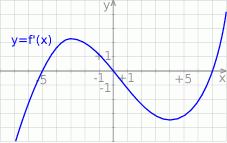
Wynika stąd, że
A) 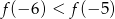 B)
B) 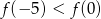 C)
C) 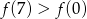 D)
D) 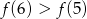
Dziedziną funkcji 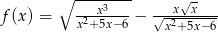 jest
jest
A) 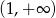 B)
B) 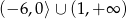 C)
C) 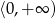 D)
D) 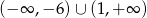
Zadania otwarte
Oblicz granicę jednostronną 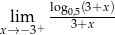 .
.
Z wierzchołków czworokąta 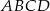 poprowadzono półproste, które przecinają się w wierzchołkach czworokąta
poprowadzono półproste, które przecinają się w wierzchołkach czworokąta 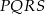 wpisanego w okrąg (zobacz rysunek).
wpisanego w okrąg (zobacz rysunek).
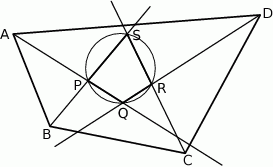
Wykaż, że jeżeli półproste 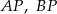 i
i 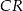 są dwusiecznymi odpowiednio kątów
są dwusiecznymi odpowiednio kątów 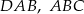 i
i 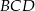 , to półprosta
, to półprosta 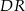 jest dwusieczną kąta
jest dwusieczną kąta 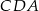 .
.
Wykaż, że jeżeli wielomian 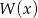 jest podzielny przez
jest podzielny przez 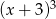 , to wielomian
, to wielomian 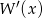 jest podzielny przez
jest podzielny przez 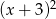 .
.
Rozwiąż równanie 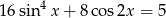 w przedziale
w przedziale 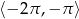 .
.
Funkcja 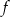 określona jest wzorem
określona jest wzorem 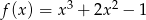 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 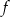 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 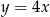 .
.
Pole trapezu równoramiennego opisanego na okręgu jest równe 80, a cosinus kąta rozwartego tego trapezu jest równy 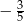 . Oblicz długość ramienia tego trapezu.
. Oblicz długość ramienia tego trapezu.
W pierwszej urnie umieszczono 5 kul białych i 4 kule czarne, a w drugiej urnie 6 kul białych i 7 kul czarnych. Losujemy jedną kulę z pierwszej urny, przekładamy ją do urny drugiej i dodatkowo wyjmujemy z drugiej urny jeszcze dwie kule koloru innego, niż kolor wylosowanej kuli. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że obie kule wylosowane z drugiej urny będą czarne.
Dla jakich wartości parametru 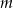 jeden z pierwiastków równania
jeden z pierwiastków równania 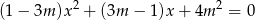 jest połową drugiego pierwiastka?
jest połową drugiego pierwiastka?
Wyznacz równanie okręgu wpisanego w deltoid, którego boki są zawarte w prostych o równaniach 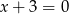 ,
, 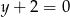 ,
, 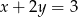 i
i 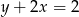 .
.
Podstawą ostrosłupa 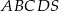 jest czworokąt
jest czworokąt 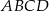 . Przekątna
. Przekątna 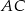 tego czworokąta ma długość
tego czworokąta ma długość 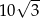 , a kąt
, a kąt 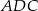 ma miarę
ma miarę 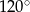 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 26. Oblicz odległość środka wysokości tego ostrosłupa od krawędzi
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 26. Oblicz odległość środka wysokości tego ostrosłupa od krawędzi 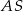 .
.
Podstawą prostopadłościanu jest prostokąt, w którym jeden bok jest dwa razy dłuższy od drugiego. Pole powierzchni całkowitej tego prostopadłościanu jest równe 1. Jakie powinny być wymiary tego prostopadłościanu, aby jego objętość była największa? Oblicz tę największą objętość.

