/Szkoła średnia/Zadania maturalne
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom podstawowy grupa I 6 czerwca 2012 Czas pracy: 170 minut
Zadania zamknięte
Dane są zbiory liczbowe 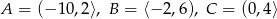 . Wynikiem działań
. Wynikiem działań 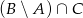 jest zbiór
jest zbiór
A) 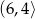 B)
B) 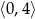 C)
C) 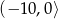 D)
D) 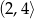
Wartość wyrażenia 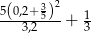 wynosi
wynosi
A) 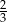 B)
B) 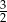 C)
C) 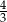 D)
D) 
Liczbą odwrotną do liczby 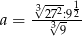 jest
jest
A) 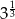 B)
B) 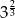 C)
C) 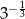 D)
D) 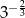
Jeden bok kwadratu o polu 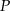 zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
A) 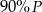 B)
B) 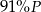 C)
C) 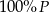 D)
D) 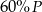
Wartość liczbowa wyrażenia 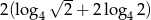 jest równa
jest równa
A) 1,5 B) 2 C) 2,5 D) 3
Ile rozwiązań ma układ równań 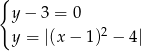
A) 1 B) 2 C) 3 D) 4
Rozwiązaniem nierówności 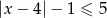 jest zbiór
jest zbiór
A) 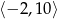 B)
B) 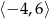 C)
C) 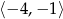 D)
D) 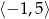
Zbiorem wartości funkcji 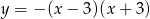 określonej dla
określonej dla 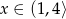 jest przedział
jest przedział
A) 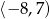 B)
B) 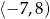 C)
C) 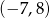 D)
D) 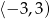
Jeżeli proste 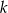 i
i 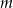 są równoległe (patrz rysunek), to długość odcinka
są równoległe (patrz rysunek), to długość odcinka  wynosi
wynosi
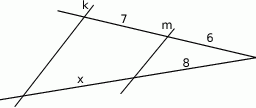
A) 9 B) 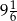 C)
C) 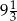 D)
D) 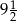
Wskaż równanie prostej prostopadłej do prostej o równaniu 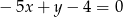 .
.
A) 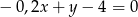 B)
B) 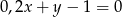 C)
C) 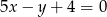 D)
D) 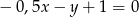
Rozwiązaniem równania 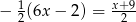 jest liczba
jest liczba
A) 1 B) 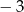 C)
C) 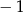 D) 3
D) 3
20% pola ograniczonego okręgiem o równaniu 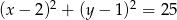 wynosi
wynosi
A) 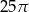 B)
B) 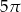 C)
C) 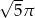 D)
D) 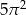
Osią symetrii paraboli określonej wzorem 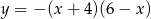 jest prosta o równaniu
jest prosta o równaniu
A) 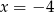 B)
B) 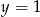 C)
C) 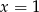 D)
D) 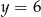
Funkcja 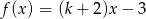 jest malejąca jeśli
jest malejąca jeśli
A) 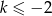 B)
B) 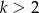 C)
C) 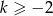 D)
D) 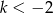
Pole rombu o boku równym 13 cm i kącie rozwartym wynoszącym 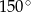 wynosi
wynosi
A) 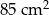 B)
B) 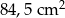 C)
C) 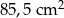 D)
D) 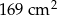
Długości boków trójkąta wychodzących z wierzchołka kąta ostrego  wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt
wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt  , jeśli pole tego trójkąta jest równe
, jeśli pole tego trójkąta jest równe 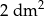 ?
?
A) 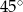 B)
B) 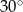 C)
C) 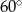 D)
D) 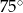
Wartość liczbowa wyrażenia 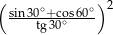 wynosi
wynosi
A) 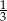 B)
B) 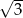 C) 3 D)
C) 3 D) 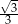
Jeżeli punkty 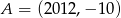 i
i 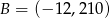 są końcami odcinka
są końcami odcinka 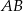 , to środkiem tego odcinka jest punkt o współrzędnych
, to środkiem tego odcinka jest punkt o współrzędnych
A) 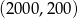 B)
B) 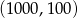 C)
C) 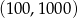 D)
D) 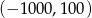
Proste o równaniach 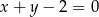 i
i 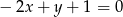 przecinają się w punkcie o współrzędnych
przecinają się w punkcie o współrzędnych
A) 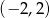 B)
B) 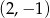 C)
C) 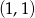 D)
D) 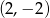
Wierzchołek paraboli opisanej wzorem 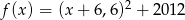 należy do
należy do
A) I ćwiartki układu współrzędnych
B) II ćwiartki układu współrzędnych
C) III ćwiartki układu współrzędnych
D) IV ćwiartki układu współrzędnych
Rozwiązaniem równania 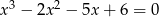 nie jest liczba
nie jest liczba
A) 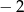 B) 1 C) 4 D) 3
B) 1 C) 4 D) 3
Kąt 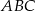 (patrz rysunek) ma miarę
(patrz rysunek) ma miarę
A) 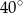 B)
B) 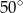 C)
C) 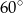 D)
D) 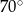
Dla jakiej wartości parametru  , miejscem zerowym funkcji
, miejscem zerowym funkcji 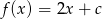 jest liczba
jest liczba 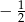 ?
?
A) 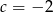 B)
B) 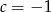 C)
C) 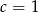 D)
D) 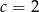
Zadania otwarte
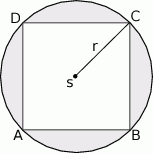
Na kwadracie 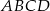 opisano okrąg o promieniu
opisano okrąg o promieniu 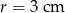 . Oblicz pole zacieniowanej figury.
. Oblicz pole zacieniowanej figury.
Rozwiąż nierówność 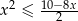 .
.
Przymocowana do podłoża lina o długości 16 m podtrzymuje pionowy maszt. Na jakiej wysokości lina jest przymocowana do masztu jeżeli kąt nachylenia do powierzchni ziemi wynosi 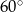 ?
?
Wykaż, że różnica kwadratów dwóch kolejnych liczb nieparzystych jest liczbą podzielną przez 8.
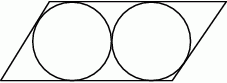
W równoległoboku wpisano dwa przystające okręgi styczne zewnętrznie do siebie (patrz rysunek). Wykaż, że średnica każdego z tych okręgów jest równa różnicy długości dłuższego i krótszego boku tego równoległoboku.
Dany jest trójkąt o przyprostokątnych 12 i 5. Wyznacz promień okręgu wpisanego w ten trójkąt.
Suma cyfr liczby trzycyfrowej podzielnej przez 5 jest równa 17. Jeśli zapiszemy cyfry tej liczby w przeciwnej kolejności, to otrzymamy liczbę o 99 większą od początkowej. Wyznacz liczbę początkową.
Dwóch motocyklistów wyrusza jednocześnie z tego samego miejsca. Jeden porusza się z prędkością 60 km/h i jedzie w kierunku wschodnim, a drugi z prędkością 80 km/h jedzie na północ. Po jakim czasie odległość między nimi (mierzona w linii prostej) będzie równa 300 km?
Na rysunku przedstawiony jest wykres funkcji 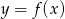 .
.
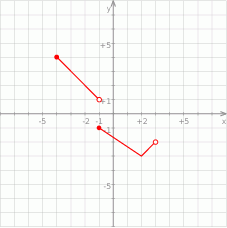
- Podaj zbiór wartości tej funkcji.
- Podaj dziedzinę tej funkcji.
- Wartość funkcji dla argumentu 2.
- Narysuj wykres funkcji
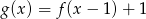 .
. - Narysuj wykres symetryczny do wykresu funkcji
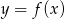 względem początku układu współrzędnych.
względem początku układu współrzędnych.

