/Szkoła średnia/Zadania maturalne
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 28 kwietnia 2012 Czas pracy: 170 minut
Zadania zamknięte
Rozwiązaniem równania 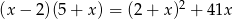 jest:
jest:
A) 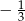 B)
B) 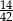 C)
C) 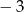 D)
D) 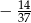
Liczba 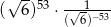 jest równa
jest równa
A) 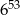 B)
B) 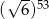 C) 1 D) 0
C) 1 D) 0
Cenę aparatu, który początkowo kosztował 2000 zł dwukrotnie podniesiono o 10%, a następnie dwukrotnie obniżono o 10%. Po tych zmianach ceny aparat kosztował
A) 1620 zł B) 1960,2 zł C) 2000 zł D) 1980 zł
Wyrażenie 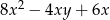 jest równe iloczynowi
jest równe iloczynowi
A) 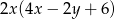 B)
B) 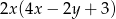 C)
C) 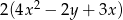 D)
D) 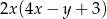
Największą liczbą całkowitą należącą do zbioru rozwiązań nierówności 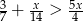 jest
jest
A) 1 B) 0 C) 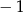 D)
D) 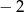
Która z liczb jest równa 3?
A) 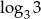 B)
B) 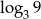 C)
C) 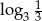 D)
D) 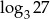
Liczba 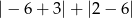 jest równa
jest równa
A) 7 B) 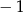 C) 1 D)
C) 1 D) 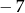
Równanie 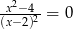
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie trzy rozwiązania
Zbiorem rozwiązań nierówności 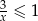 jest
jest
A) 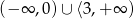 B)
B) 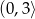 C)
C) 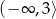 D)
D) 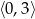
Najmniejszą wartość w przedziale 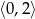 funkcja kwadratowa
funkcja kwadratowa 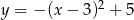 przyjmuje dla argumentu
przyjmuje dla argumentu
A) 2 B) 0 C) 3 D) 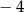
Prosta o równaniu 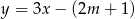 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 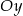 w punkcie
w punkcie 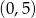 . Wtedy
. Wtedy
A) 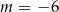 B)
B) 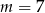 C)
C) 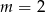 D)
D) 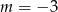
W ciągu geometrycznym 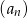 dane są
dane są 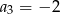 i
i 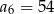 . Wtedy
. Wtedy
A) 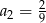 B)
B) 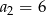 C)
C) 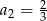 D)
D) 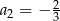
Wiadomo, że 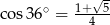 . Zatem
. Zatem
A) 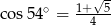 B)
B) 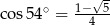 C)
C) 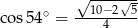 D)
D) 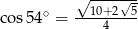
Rysunek przedstawia wykres funkcji 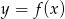 .
.
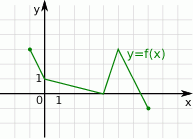
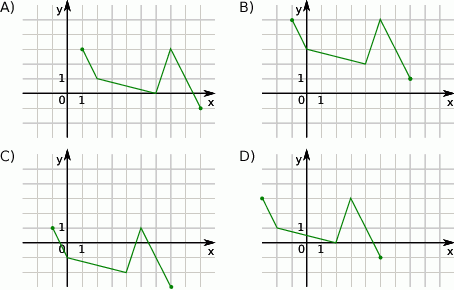
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 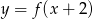 .
.
W trójkącie 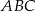 poprowadzono odcinek
poprowadzono odcinek 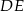 równoległy do boku
równoległy do boku 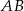 w ten sposób, że
w ten sposób, że 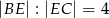 .
.
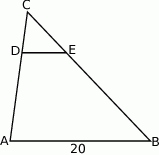
Jeżeli 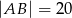 to długość odcinka
to długość odcinka 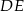 jest równa
jest równa
A) 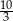 B) 4 C) 5 D)
B) 4 C) 5 D) 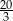
Ile wyrazów ujemnych ma ciąg 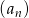 określony wzorem
określony wzorem 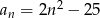 dla
dla 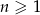 ?
?
A) 0 B) 1 C) 2 D) 3
Średnia arytmetyczna liczb: 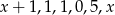 jest równa
jest równa  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 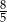 B) 2 C)
B) 2 C) 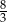 D)
D) 
Wysokość rombu o boku długości 8 i kącie ostrym 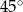 jest równa
jest równa
A) 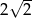 B) 4 C)
B) 4 C) 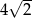 D) 8
D) 8
Środek 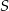 okręgu o równaniu
okręgu o równaniu 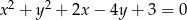 ma współrzędne
ma współrzędne
A) 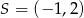 B)
B) 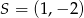 C)
C) 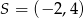 D)
D) 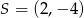
Kula ma objętość 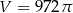 . Promień
. Promień  tej kuli jest równy
tej kuli jest równy
A) 6 B) 8 C) 9 D) 12
Kąt wpisany w okrąg o promieniu 9 ma miarę 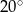 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 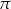 B)
B) 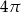 C)
C) 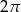 D)
D) 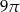
Latawiec ma wymiary podane na rysunku. Powierzchnia zacieniowanego trójkąta jest równa
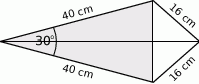
A) 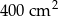 B)
B) 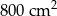 C)
C) 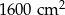 D)
D) 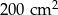
Pole powierzchni całkowitej sześcianu jest równe 48. Długość przekątnej tego sześcianu jest równa
A) 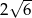 B)
B) 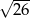 C) 4 D)
C) 4 D) 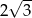
Zadania otwarte
Rozwiąż nierówność 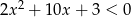 .
.
Dany ciąg arytmetyczny 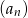 taki, że
taki, że 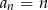 , dla
, dla 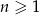 . Udowodnij, że iloczyn każdych dziesięciu kolejnych wyrazów tego ciągu jest podzielny przez
. Udowodnij, że iloczyn każdych dziesięciu kolejnych wyrazów tego ciągu jest podzielny przez 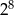 .
.
Liczby 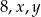 w podanej kolejności tworzą ciąg arytmetyczny, przy czym
w podanej kolejności tworzą ciąg arytmetyczny, przy czym 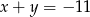 . Oblicz
. Oblicz  i
i 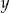 .
.
Oblicz  z równania
z równania 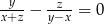 i przedstaw wynik w najprostszej postaci.
i przedstaw wynik w najprostszej postaci.
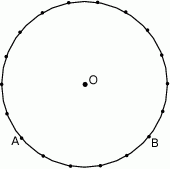
Punkty 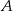 i
i 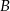 leżą na okręgu o środku
leżą na okręgu o środku 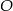 i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 13:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 13:5. Oblicz miarę kąta środkowego opartego na krótszym łuku.
Trójkąty 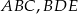 i
i 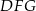 są równoboczne oraz
są równoboczne oraz 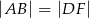 . Punkty
. Punkty 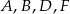 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 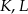 i
i 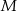 są środkami odcinków
są środkami odcinków 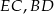 i
i 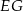 . Wykaż, że punkty
. Wykaż, że punkty 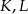 i
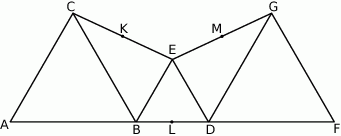
i 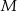 są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.
Ile jest liczb pięciocyfrowych, spełniających jednocześnie następujące cztery warunki:
(1) w zapisie tej liczby nie występuje cyfra 4,
(2) cyfry setek, dziesiątek i jedności są nieparzyste,
(3) cyfra setek jest mniejsza od cyfry dziesiątek,
(4) cyfra dziesiątek jest mniejsza od cyfry jedności.
Dwóch turystów przebyło tę samą trasę o długości 84 km, przy czym każdy z nich przechodził dziennie tę samą liczbę kilometrów. Pokonanie tej trasy zajęło drugiemu turyście o 3 dni dłużej niż pierwszemu, a pierwszy turysta przechodził dziennie o 9 km więcej od drugiego. Oblicz, ile kilometrów dziennie przechodził każdy z turystów.
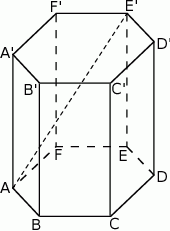
Przekątna 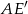 graniastosłupa prawidłowego sześciokątnego ma długość
graniastosłupa prawidłowego sześciokątnego ma długość 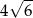 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem 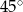 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.